题目内容
已知二次函数f(x)=x2+px+q,不等式f(x)<0的解集是(-2,3)
(1)求实数p和q的值;
(2)解不等式qx2+px+1>0.
(1)求实数p和q的值;
(2)解不等式qx2+px+1>0.
考点:二次函数的性质
专题:函数的性质及应用
分析:(1)直接将-2,3代入方程由韦达定理求出p,q的值,(2)将p,q代入解不等式即可.
解答:
解:(Ⅰ)由不等式f(x)<0的解集是{x|-2<x<3}
∴-2,3是方程x2+px+q=0的两根,
∴-p=-2+3,q=-2×3,
即:p=-1,q=-6,
(Ⅱ)不等式等价于-6x2-x+1>0,
即:6x2+x-1<0,
∴(3x-1)(2x+1)<0,
∴-
<x<
,
不等式的解集为:{x|-
<x<
}.
∴-2,3是方程x2+px+q=0的两根,
∴-p=-2+3,q=-2×3,
即:p=-1,q=-6,
(Ⅱ)不等式等价于-6x2-x+1>0,
即:6x2+x-1<0,
∴(3x-1)(2x+1)<0,
∴-
| 1 |
| 2 |
| 1 |
| 3 |
不等式的解集为:{x|-
| 1 |
| 2 |
| 1 |
| 3 |
点评:本题查考察了二次函数的性质,韦达定理,解一元二次不等式,是一道基础题.

练习册系列答案
相关题目
已知函数f(x)是偶函数,且∫
f(x)dx=4,则∫
f(x)=( )
6 0 |
6 -6 |
| A、0 | B、2 | C、4 | D、8 |
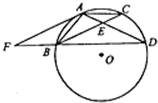 如图,点A,B,C,D在⊙O上,AB=AC,AD与BC相交于点E,AE=
如图,点A,B,C,D在⊙O上,AB=AC,AD与BC相交于点E,AE=