题目内容
7.已知函数f(x)=ax+(1-a)lnx+$\frac{1}{x}$,(a∈R).(1)当a=0时,求f(x)的极值;
(2)当a<0时,求f(x)的单调区间.
分析 (1)求导数,确定函数的单调性,即可求函数f(x)的极值;(2)求出函数的导数,通过讨论a的范围,从而确定函数的单调区间.
解答 解:a=0时,f(x)=lnx+$\frac{1}{x}$,
∴f′(x)=$\frac{x-1}{{x}^{2}}$,
令f′(x)=0,得x=1,
又f(x)的定义域为(0,+∞),
f′(x),f(x)随x的变化情况如下表:
| x | (0,1) | 1 | (1,+∞) |
| f′(x) | - | 0 | + |
| f(x) | 极小值 |
(2)f′(x)=a+$\frac{1-a}{x}$-$\frac{1}{{x}^{2}}$=$\frac{(ax+1)(x-1)}{{x}^{2}}$(x>0,a<0),
-1≤a<0时,-$\frac{1}{a}$≥1,
令f′(x)>0,解得:1<x<-$\frac{1}{a}$,
令f′(x)<0,解得:x<1或x>-$\frac{1}{a}$,
∴f(x)在(0,1)递减,在(1,-$\frac{1}{a}$)递增,在(-$\frac{1}{a}$,+∞)递减;
a<-1时,-$\frac{1}{a}$<1,
令f′(x)>0,解得:-$\frac{1}{a}$<x<1,
令f′(x)<0,解得:x<-$\frac{1}{a}$或x>1,
∴f(x)在(0,-$\frac{1}{a}$)递减,在(-$\frac{1}{a}$,1)递增,在(1,+∞)递减.
点评 本题考查函数的单调性与极值,考查学生的计算能力,考察分类讨论,是一道中档题.

练习册系列答案
相关题目
2.已知四棱锥P-ABCD中,底面ABCD是正方形,边长为4,PA=PD=$\sqrt{13}$,侧面PAD⊥底面ABCD,在四棱锥内放一个球,要使它的体积最大,则球的半径为( )
| A. | 3 | B. | 2 | C. | 1 | D. | $\frac{\sqrt{2}}{2}$ |
19.某几何体的三视图如图所示,当a+b取最大值时,该几何体体积为( )
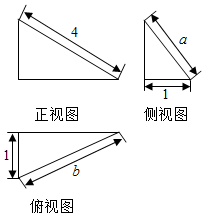

| A. | $\frac{4}{3}$ | B. | $\frac{8}{9}$ | C. | $\frac{4}{9}$ | D. | $\frac{16}{9}$ |
17.已知三点(2,3),(6,5),(4,b)共线,则实数b的值为( )
| A. | 4 | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | -2 |
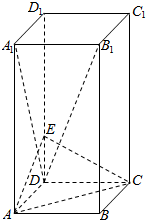 如图,长方体ABCD-A1B1C1D1中,底面ABCD是正方形,AA1=2AB=2,E是DD1上的一点,且满足B1D⊥平面ACE.
如图,长方体ABCD-A1B1C1D1中,底面ABCD是正方形,AA1=2AB=2,E是DD1上的一点,且满足B1D⊥平面ACE.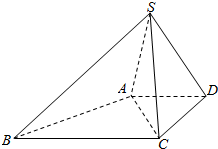 如图,在底面为梯形的四棱锥S-ABCD中,已知AD∥BC,∠ASC=60°,AD=DC=$\sqrt{2}$,SA=SC=SD=2.
如图,在底面为梯形的四棱锥S-ABCD中,已知AD∥BC,∠ASC=60°,AD=DC=$\sqrt{2}$,SA=SC=SD=2.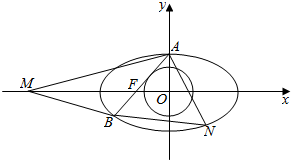 如图,椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)和圆C2:x2+y2=$\frac{{b}^{2}}{2}$,椭圆C1短轴的上端点为A,左焦点为F,直线AF与圆C2相切,椭圆C1左焦点到左准线的距离为1.
如图,椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)和圆C2:x2+y2=$\frac{{b}^{2}}{2}$,椭圆C1短轴的上端点为A,左焦点为F,直线AF与圆C2相切,椭圆C1左焦点到左准线的距离为1.