题目内容
已知100件产品中有97件正品和3件次品,现从中任意抽出3件产品进行检查,则恰好抽出2件次品的抽法种数是( )
A、C
| ||||
B、A
| ||||
C、C
| ||||
D、A
|
考点:排列、组合及简单计数问题
专题:计算题,排列组合
分析:事件分两步完成,第一步从3件次品中抽取2件次品,第二步从97件正品中抽取1件正品,根据乘法原理计算求得.
解答:
解:∵100件产品中有97件正品和3件次品,从中任意抽出3件产品进行检查,
∴其中恰好抽出2件次品的抽法有C
C
.
故选:C.
∴其中恰好抽出2件次品的抽法有C
2 3 |
1 97 |
故选:C.
点评:本题考查计数原理及应用,考查排列组合的实际应用,解题时要认真审题.

练习册系列答案
相关题目
设F1,F2分别是双曲线
-
=1(a>0,b>0)的左、右焦点,若双曲线左支上存在一点M使
•(
+
)=0,O坐标原点,且|
|=
|
|,则该双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| F1M |
| OM |
| OF1 |
| MF1 |
| ||
| 3 |
| MF2 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
已知i是虚数单位,则
=( )
| 2+i |
| 1+i |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
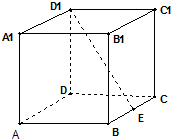 如图在棱长为2的正方体ABCD-A1B1C1D1中E为BC的中点,点P在线段D1E上,点P到直线CC1的距离的最小值为( )
如图在棱长为2的正方体ABCD-A1B1C1D1中E为BC的中点,点P在线段D1E上,点P到直线CC1的距离的最小值为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 函数f(x)的定义域为[-2,0)∪(0,2],图象如图,则不等式f(x)-f(-x)≤4的解集是( )
函数f(x)的定义域为[-2,0)∪(0,2],图象如图,则不等式f(x)-f(-x)≤4的解集是( )| A、[-1,0) |
| B、[-2,-1)∪(0,2] |
| C、[-2,-1]∪(0,2] |
| D、[-2,0)∪(0,1] |
从0,1,2,3中选取三个不同的数字组成一个三位数,则不同的三位数有( )
| A、24个 | B、20个 |
| C、18个 | D、15个 |