题目内容
直线2kx+y-6k+1=0（k∈R）经过定点P，则P为（ ）
| A、（1，3） |
| B、（3，1） |
| C、（-1，-3） |
| D、（3，-1） |
考点：恒过定点的直线
专题：直线与圆
分析：直线2kx+y-6k+1=0（k∈R）的方程可化为y+1=-2k（x-3），根据x=3，y=-1时方程恒成立，可知直线过定点的坐标．
解答：
解：∵直线2kx+y-6k+1=0（k∈R）的方程
可化为y+1=-2k（x-3），
当x=3，y=-1时方程恒成立，
∴直线过定点（3，-1）
故选D．
可化为y+1=-2k（x-3），
当x=3，y=-1时方程恒成立，
∴直线过定点（3，-1）
故选D．
点评：本题考查的知识点是恒过定义的直线，解答的关键是将参数分离，化为y-y0=k（x-x0）形式，令y-y0，x-x0=0可得答案
练习册系列答案
夺冠金卷全能练考系列答案
相关题目
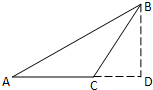已知△ABC为等腰三角形，∠A=∠B=30°，BD为AC边上的高，若| AB |
| a |
| AC |
| b |
| BD |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
已知函数f(x)=
的定义域为R，则（ ）
| cos(sinx) |
| A、f（x）是奇函数 |
| B、f（x）是偶函数 |
| C、f（x）即是奇函数又是偶函数 |
| D、f（x）即不是奇函数又不是偶函数 |
设a，b，c∈R，且a＜b，则（ ）
| A、ac＞bc | ||||
B、
| ||||
| C、a2＞b2 | ||||
| D、a3＜b3 |
已知奇函数f（x）在区间[-2，2]上单调递减，则不等式f（x2）+f（2x）＞0的解集是（ ）
| A、[-1，0） |
| B、（-2，0） |
| C、（-2，-1] |
| D、（-∞，-2）∪（0，+∞） |