题目内容
14.已知A,B是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的两个焦点,点C在双曲线上,在△ABC中,sinA:sinB=3:1,则该双曲线的离心率的取值范围为( )| A. | $(1,\sqrt{3)}$ | B. | $({1,\frac{{\sqrt{10}}}{2}}]$ | C. | (1,2) | D. | (1,2] |
分析 利用正弦定理,结合双曲线的定义,得出e<2,结合e>1,即可得出结论.
解答 解:由题意,|CB|=3|CA|,
∵|CB|-|CA|=2a,
∴|CA|=a,
∵|CA|>c-a,
∴a>c-a,
∴e<2,
∵e>1,
∴1<e<2.
故选C.
点评 本题考查正弦定理,双曲线的定义与性质,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
4.已知集合A={x|x2-x-6<0},B={x|x2+2x-8>0},则A∩B=( )
| A. | (-2,3) | B. | (-4,2) | C. | (-4,3) | D. | (2,3) |
19.若不等式x2-2x+a>0恒成立,则a的取值范围是( )
| A. | a<0 | B. | a<1 | C. | a>0 | D. | a>1 |
20.下列函数中哪个与函数y=x相等( )
| A. | y=($\sqrt{x}$)2 | B. | f(x)=$\frac{{x}^{2}}{x}$ | C. | y=|x| | D. | y=$\root{3}{{x}^{3}}$ |
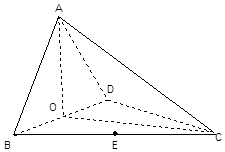 如图,四面体ABCD中,O、E分别是BD、BC的中点,底面BCD是正三角形,AC=BD=2,AB=AD=$\sqrt{2}$.
如图,四面体ABCD中,O、E分别是BD、BC的中点,底面BCD是正三角形,AC=BD=2,AB=AD=$\sqrt{2}$.