题目内容
14.已知函数f(x)=3x-2mx2-3ln(x+1),其中m∈R(1)若x=1是f(x)的极值点,求m的值;
(2)若0<m<$\frac{3}{4}$,求f(x)的单调区间;
(3)若f(x)在[0,+∞)上的最小值是0,求m的取值范围.
分析 (1)求出函数的导数,根据f′(1)=0,求出m的值即可;
(2)求出函数的导数,根据m的范围,解关于导函数的不等式,求出函数的单调区间即可;
(3)求出函数的导数,通过讨论m的范围确定函数的单调性,从而得到m的范围即可.
解答 解:(1)f(x)=3x-2mx2-3ln(x+1)的定义域是(-1,+∞),
f′(x)=3-4mx-$\frac{3}{x+1}$,f′(1)=3-4m-$\frac{3}{2}$=0,解得:m=$\frac{3}{8}$;
(2)f′(x)=3-4mx-$\frac{3}{x+1}$=$\frac{-4{mx}^{2}+(3-4m)x}{x+1}$,
∵0<m<$\frac{3}{4}$,∴$\frac{3-4m}{4m}$>0,
令f′(x)<0,解得:x>$\frac{3-4m}{4m}$或x<0,
令f′(x)>0,解得:0<x<$\frac{3-4m}{4m}$,
故f(x)在(-1,0)递减,在(0,$\frac{3-4m}{4m}$)递增,在($\frac{3-4m}{4m}$,+∞)递减;
(3)f′(x)=3-4mx-$\frac{3}{x+1}$=$\frac{-4{mx}^{2}+(3-4m)x}{x+1}$,
由(2)得:m>0时,显然不合题意,
m=0时,f′(x)=$\frac{3x}{x+1}$,f(x)在[0,+∞)递增,
f(x)的最小值是f(0)=0,符合题意,
m<0时,f′(x)>0,f(x)在[0,+∞)递增,
f(x)的最小值是f(0)=0,符合题意,
故m≤0.
点评 本题考查了切线方程问题,考查函数的单调性、最值问题,考查导数的应用,是一道中档题.

练习册系列答案
相关题目
8.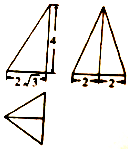 若一个几何体的三视图如图所示,则这个几何体的外接球的表面积为( )
若一个几何体的三视图如图所示,则这个几何体的外接球的表面积为( )
 若一个几何体的三视图如图所示,则这个几何体的外接球的表面积为( )
若一个几何体的三视图如图所示,则这个几何体的外接球的表面积为( )| A. | 34π | B. | $\frac{80π}{3}$ | C. | $\frac{91}{3}π$ | D. | 114π |
9.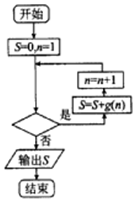 已知函数f(x)=ax3+$\frac{1}{2}$x2在x=-1处取得极大值,记g(x)=$\frac{1}{f′(x)}$.程序框图如图所示,若输出的结果S>$\frac{2014}{2015}$,则判断框中可以填入的关于n的判断条件是( )
已知函数f(x)=ax3+$\frac{1}{2}$x2在x=-1处取得极大值,记g(x)=$\frac{1}{f′(x)}$.程序框图如图所示,若输出的结果S>$\frac{2014}{2015}$,则判断框中可以填入的关于n的判断条件是( )
 已知函数f(x)=ax3+$\frac{1}{2}$x2在x=-1处取得极大值,记g(x)=$\frac{1}{f′(x)}$.程序框图如图所示,若输出的结果S>$\frac{2014}{2015}$,则判断框中可以填入的关于n的判断条件是( )
已知函数f(x)=ax3+$\frac{1}{2}$x2在x=-1处取得极大值,记g(x)=$\frac{1}{f′(x)}$.程序框图如图所示,若输出的结果S>$\frac{2014}{2015}$,则判断框中可以填入的关于n的判断条件是( )| A. | n≤2014? | B. | n≤2015? | C. | n>2014? | D. | n>2015? |
19.若不等式x2-2x+a>0恒成立,则a的取值范围是( )
| A. | a<0 | B. | a<1 | C. | a>0 | D. | a>1 |