题目内容
4.已知f(x)=|x-2017|+|x-2016|+…+|x-1|+|x+1|+…+|x+2017|(x∈R),且满足f(a2-3a+2)=f(a-1)的整数a共有n个,g(x)=$\frac{{x}^{2}({x}^{2}+{k}^{2}+2k-4)+4}{({x}^{2}+2)^{2}-2{x}^{2}}$的最小值为m,且m+n=3,则实数k的值为0或-2.分析 根据已知,可以求出函数为一个偶函数,则f(a2-3a+2)=f(a-1),可以转化为|a2-3a+2|=|a-1|,由绝对值的几何意义,我们可得a,即可求出n,m,进而化简函数,即可得出结论.
解答 解:根据绝对值的几何意义可知f(-x)=f(x),即函数f(x)是偶函数,
若f(a2-3a+2)=f(a-1),
则a2-3a+2=a-1,①或a2-3a+2=-(a-1),②,
由①得a2-3a+2=(a-1)(a-2)=a-1,
即(a-1)(a-3)=0,解得a=1或a=3.
由②得a2-3a+2=(a-1)(a-2)=-(a-1),
即(a-1)(a-1)=0,解得a=1.
综上a=1或a=3,
又∵f(0)=f(1)=f(-1)
∴当a=2时,也满足要求,
则a的值有3个,即n=3,
∵m+n=3,∴m=0,
g(x)=$\frac{{x}^{2}({x}^{2}+{k}^{2}+2k-4)+4}{({x}^{2}+2)^{2}-2{x}^{2}}$=1+$\frac{{k}^{2}+2k-6}{{x}^{2}+\frac{4}{{x}^{2}}+2}$的最小值为m=0,可得k2+2k-6=-6,
∴k=0或-2
故答案为0或-2.
点评 本题考查的知识点是函数奇偶性的性质,及绝对值的几何意义,解答本题的技巧性较强,难度也比较大,其中分析出函数的奇偶性,从面将f(a2-3a+2)=f(a-1),转化为一个绝对值方程是解答本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.高三某班要安排6名同学值日(周日休息),每天安排一人,每人值日一天,要求甲必须安排在周一到周四的某一天,乙必须安排在周五或周六的某一天,则不同的值日生表有多少种?( )
| A. | 144 | B. | 192 | C. | 360 | D. | 720 |
19.若不等式x2-2x+a>0恒成立,则a的取值范围是( )
| A. | a<0 | B. | a<1 | C. | a>0 | D. | a>1 |
9.若全集U={1,2,3,4,5},集合M={1,2},N={2,3,4},则(∁UM)∩N等于( )
| A. | {1} | B. | {2} | C. | {3,4} | D. | {5} |
14.函数f(x)=|${log_{\frac{1}{2}}}$x|的单调递增区间是( )
| A. | $(0,\frac{1}{2}]$ | B. | (1,2] | C. | [1,+∞) | D. | (0,+∞) |
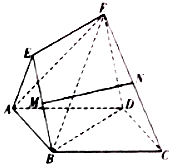 如图5所示,四边形ABCD是边长为2的正方形,四边形BDFE是平行四边形,点M,N分别是BE,CF的中点.
如图5所示,四边形ABCD是边长为2的正方形,四边形BDFE是平行四边形,点M,N分别是BE,CF的中点.