题目内容
11.若函数f(x)满足关系式f(x)+2f(1-x)=-$\frac{3}{x}$,则f(2)的值为( )| A. | $-\frac{3}{2}$ | B. | $\frac{3}{2}$ | C. | $-\frac{5}{2}$ | D. | $\frac{5}{2}$ |
分析 利用赋值法求解即可.
解答 解:∵f(x)+2f(1-x)=-$\frac{3}{x}$,
令x=2,则有f(2)+2f(-1)=-$\frac{3}{2}$….①
令x=-1,则有f(-1)+2f(2)=3…②
由①②解得f(2)=$\frac{5}{2}$,
故选D.
点评 本题考查了赋值法的运用和计算.属于基础题.

练习册系列答案
相关题目
19.若不等式x2-2x+a>0恒成立,则a的取值范围是( )
| A. | a<0 | B. | a<1 | C. | a>0 | D. | a>1 |
20.下列函数中哪个与函数y=x相等( )
| A. | y=($\sqrt{x}$)2 | B. | f(x)=$\frac{{x}^{2}}{x}$ | C. | y=|x| | D. | y=$\root{3}{{x}^{3}}$ |
1.有下列四个命题,其中假命题是( )
| A. | ?x0>0,x02≤x0 | B. | ?x∈R,3x>0 | ||
| C. | ?x0∈R,sinx0+cosx0=2 | D. | ?x0∈R,lgx0=0 |
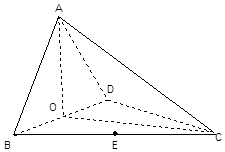 如图,四面体ABCD中,O、E分别是BD、BC的中点,底面BCD是正三角形,AC=BD=2,AB=AD=$\sqrt{2}$.
如图,四面体ABCD中,O、E分别是BD、BC的中点,底面BCD是正三角形,AC=BD=2,AB=AD=$\sqrt{2}$.