题目内容
数列1,2,2,3,3,3,4,4,4,4,…的第15项是 .
考点:数列的概念及简单表示法
专题:等差数列与等比数列,推理和证明
分析:由已知中数列1,2,2,3,3,3,4,4,4,4,…有1项1,2项2,3项3,…n项n,此时共有1+2+3+…+n=
项,进而可得第15项的值.
| n(n+1) |
| 2 |
解答:
解:∵数列1,2,2,3,3,3,4,4,4,4,…
有1项1,2项2,3项3,…n项n,
累加值从1到n,共有1+2+3+…+n=
项,
令
≤15,
解得:n≤5.
故数列的第15项是:5,
故答案为:5
有1项1,2项2,3项3,…n项n,
累加值从1到n,共有1+2+3+…+n=
| n(n+1) |
| 2 |
令
| n(n+1) |
| 2 |
解得:n≤5.
故数列的第15项是:5,
故答案为:5
点评:归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想).

练习册系列答案
相关题目
已知函数f(x)=x3+x,则不等式f(
)>f(x-1)的解集是( )
| 2 |
| x |
| A、(-∞,-1]∪(0,2) |
| B、(-∞,-1)∪(0,2) |
| C、(-∞,-1]∪[0,2] |
| D、(-1,0)∪(2,+∞) |
对任意实数x,<x>表示不小于x的最小整数,如<1.1>=2,<-1.1>=-1,则“|x-y|<1”是“<x>=<y>”的( )条件.
| A、充分不必要 |
| B、必要不充分 |
| C、充分 |
| D、既不充分又不必要 |
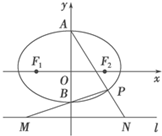 如图,椭圆
如图,椭圆