题目内容
10.已知命题p:{x||x-1|<c(c>0)},命题q:{x||x-3|>4},且¬p是q成立的充分且不必要条件,求实数c的取值范围.分析 根据绝对值不等式的解法,结合充分条件和必要条件的定义建立不等式关系进行求解即可.
解答 解:由|x-1|<c得1-c<x<1+c,即p:{x|1-c<x<1+c},¬p:{x|x>1+c或x<1-c},
由|x-3|>4,得x-3>4或x-3<-4,得x>7或x<-1,即q:{x|x>7或x<-1},
∵¬p是q成立的充分且不必要条件,
∴$\left\{\begin{array}{l}{1+c≥7}\\{1-c≤-1}\\{c>0}\end{array}\right.$得$\left\{\begin{array}{l}{c≥6}\\{c≥2}\\{c>0}\end{array}\right.$得c≥6,
即实数c的取值范围是[6,+∞).
点评 本题主要考查充分条件和必要条件的应用,根据条件建立不等式关系是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.若实数x、y满足xy>0,则$\frac{x}{x+y}$+$\frac{2y}{x+2y}$的最大值为( )
| A. | 2-$\sqrt{2}$ | B. | 2$+\sqrt{2}$ | C. | 4$-2\sqrt{2}$ | D. | 4$+2\sqrt{2}$ |
19.已知集合M={x|-$\sqrt{5}$<x<$\sqrt{3}$,x∈Z},则下列集合是集合M的子集的为( )
| A. | P={-3,0,1} | B. | Q={-1,0,1,2} | C. | R={y|-π<y<-1,y∈Z} | D. | S={x||x|≤$\sqrt{3}$,x∈N} |
16.如图示中的幂函数在第一象限的图象,则下面四个选项中正确的是( )
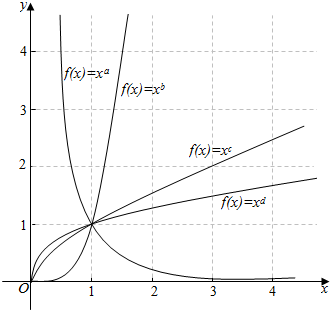

| A. | a+b+c+d为正数 | B. | b+c+d-a可能为零 | ||
| C. | a-b-c-d为负数 | D. | b×c×d×a符号不能确定 |