题目内容
7.已知函数f(x)=x2+alnx.(Ⅰ)当a=-2时,求函数f(x)的单调区间和极值;
(Ⅱ)若g(x)=f(x)+$\frac{2}{x}$在[1,+∞)上是单调增函数,求实数a的取值范围.
分析 (Ⅰ)函数f(x)的定义域为(0,+∞).当a=-2时,${f}^{'}(x)=2x-\frac{2}{x}$=$\frac{2(x+1)(x-1)}{x}$,由此利用导数性质能求出函数f(x)的单调区间和极值.
(Ⅱ) 由g(x)=x2+alnx+$\frac{2}{x}$,得${g}^{'}(x)=2x+\frac{a}{x}-\frac{2}{{x}^{2}}$,令φ(x)=$\frac{2}{x}-2{x}^{2}$,则φ′(x)=-$\frac{2}{{x}^{2}}-4x$.由此利用导数性质能求出a的取值范围.
解答 解:(Ⅰ)∵函数f(x)=x2+alnx,∴函数f(x)的定义域为(0,+∞).
当a=-2时,${f}^{'}(x)=2x-\frac{2}{x}$=$\frac{2(x+1)(x-1)}{x}$.
当x变化时,f′(x)和f(x)的值的变化情况如下表:
| x | (0,1) | 1 | (1,+∞) |
| f′(x) | - | 0 | + |
| f(x) | 递减 | 极小值 | 递增 |
(Ⅱ) 由g(x)=x2+alnx+$\frac{2}{x}$,得${g}^{'}(x)=2x+\frac{a}{x}-\frac{2}{{x}^{2}}$.
若函数g(x)为[1,+∞)上的单调增函数,则g′(x)≥0在[1,+∞)上恒成立,
即不等式2x-$\frac{2}{{x}^{2}}$+$\frac{a}{x}$≥0在[1,+∞)上恒成立.
也即a≥$\frac{2}{x}-2{x}^{2}$在[1,+∞)上恒成立.
令φ(x)=$\frac{2}{x}-2{x}^{2}$,则φ′(x)=-$\frac{2}{{x}^{2}}-4x$.
当x∈[1,+∞)时,φ′(x)=-$\frac{2}{{x}^{2}}$-4x<0,
∴φ(x)=$\frac{2}{x}-2{x}^{2}$在[1,+∞)上为减函数,∴φ(x)max=φ(1)=0.
∴a≥0.
∴a的取值范围为[0,+∞).
点评 本题考查函数的单调区间和极值的求法,考查实数的取值范围的求法,是中档题,解题时要认真审题,注意构造法和导数性质的合理运用.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
19.已知集合M={x|-$\sqrt{5}$<x<$\sqrt{3}$,x∈Z},则下列集合是集合M的子集的为( )
| A. | P={-3,0,1} | B. | Q={-1,0,1,2} | C. | R={y|-π<y<-1,y∈Z} | D. | S={x||x|≤$\sqrt{3}$,x∈N} |
2.已知双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0),右焦点F到渐近线的距离为2,F到原点的距离为3,则双曲线C的离心率e为( )
| A. | $\frac{{\sqrt{5}}}{3}$ | B. | $\frac{{3\sqrt{5}}}{5}$ | C. | $\frac{{\sqrt{6}}}{3}$ | D. | $\frac{{\sqrt{6}}}{2}$ |
12.函数g(x)=2015x+m图象不过第二象限,则m的取值范围是( )
| A. | m≤-1 | B. | m<-1 | C. | m≤-2015 | D. | m<-2015 |
16.如图示中的幂函数在第一象限的图象,则下面四个选项中正确的是( )
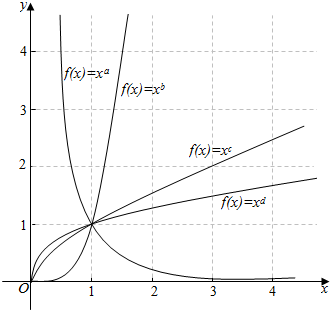

| A. | a+b+c+d为正数 | B. | b+c+d-a可能为零 | ||
| C. | a-b-c-d为负数 | D. | b×c×d×a符号不能确定 |
17.如图,在正方体ABCD-A1B1C1D1中,E为CC1的中点,则直线AE与平面ABCD所成角的正切值为( )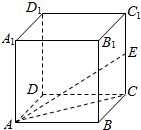

| A. | $\frac{1}{3}$ | B. | $\frac{\sqrt{2}}{4}$ | C. | $\frac{2\sqrt{2}}{3}$ | D. | 2$\sqrt{2}$ |