题目内容
3．
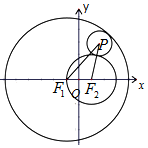已知定圆C1：（x+1）2+y2=36及定圆C2：（x-1）2+y2=4，动圆P与C1内切，与C2外切，求动圆圆心P的轨迹方程．
分析 由题意分别表示出|PF1|=6-r，|PF2|=2+r，|PF1|+|PF2|=8＞2，可知P的轨迹是以F1，F2为焦点，长轴长为8的椭圆，即可求得P的轨迹方程．
解答 解：设所求点P（x，y），F1（-1，0），F2（1，0），动圆半径为r，
由题易得|PF1|=6-r，|PF2|=2+r，
∴|PF1|+|PF2|=8＞2，
由点P到两定点F1，F2距离之和为定长8，且大于|F1F2|=2c=2，满足椭圆定义，
∴轨迹方程：$\frac{x^2}{16}+\frac{y^2}{15}=1$．
动圆圆心P的轨迹方程$\frac{x^2}{16}+\frac{y^2}{15}=1$．
点评 本题考查轨迹方程的求法，考查椭圆的定义，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
16．
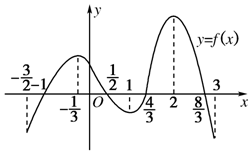函数y=f（x）在定义域$[{-\frac{3}{2}，3}]$内可导，其图象如图所示．记y=f（x）的导函数为y=f′（x），则不等式f′（x）≤0的解集为（ ）
函数y=f（x）在定义域$[{-\frac{3}{2}，3}]$内可导，其图象如图所示．记y=f（x）的导函数为y=f′（x），则不等式f′（x）≤0的解集为（ ）| A． | $[{-\frac{1}{3}，1}]∪[2，3]$ | B． | $[{-1，\frac{1}{2}}]∪[{\frac{4}{3}，\frac{8}{3}}]$ | ||
| C． | $[{-\frac{3}{2}，\frac{1}{2}}]∪[1，2）$ | D． | $[{-\frac{3}{2}，-\frac{1}{3}}]∪[{\frac{1}{2}，\frac{4}{3}}]∪[{\frac{4}{3}，3}]$ |
12．已知全集U=R，集合A={x|x2＞4}，B={x|$\frac{x+3}{x-1}$≤0}，则（∁UA）∩B等于（ ）
| A． | {x|-2≤x＜1} | B． | {x|-3≤x＜2} | C． | {x|-2≤x＜2} | D． | {x|-3≤x≤2} |