题目内容
10.设函数f(x)=$\sqrt{\frac{1+sinx}{1-sinx}}$-$\sqrt{\frac{1-sinx}{1+sinx}}$,且f(α)=1,α为第二象限角.(1)求tanα的值.
(2)求sinαcosα+5cos2α的值.
分析 (1)利用同角三角函数的基本关系,以及三角函数在各个象限中的符号,求得要求式子的值.
(2)利用同角三角函数的基本关系,求得要求式子的值.
解答 解:(1)∵函数f(x)=$\sqrt{\frac{1+sinx}{1-sinx}}$-$\sqrt{\frac{1-sinx}{1+sinx}}$,且f(α)=1,α为第二象限角.
∴$\sqrt{\frac{1+sinα}{1-sinα}}$-$\sqrt{\frac{1-sinα}{1+sinα}}$=|$\frac{1+sinα}{cosα}$|-|$\frac{1-sinα}{cosα}$|=-$\frac{1+sinα}{cosα}$-$\frac{sinα-1}{cosα}$=-2tanα=1,
∴tanα=-$\frac{1}{2}$.
(2)sinαcosα+5cos2α=$\frac{sinαcosα+{5cos}^{2}α}{{sin}^{2}α{+cos}^{2}α}$=$\frac{tanα+5}{{tan}^{2}α+1}$=$\frac{-\frac{1}{2}+5}{\frac{1}{4}+1}$=$\frac{18}{5}$.
点评 本题主要考查同角三角函数的基本关系,以及三角函数在各个象限中的符号,属于基础题.

练习册系列答案
相关题目
5.某公司13个部门接收的快递的数量如茎叶图所示,则这13个部门接收的快递的数量的中位数为( )


| A. | 6 | B. | 9 | C. | 10 | D. | 11 |
2.已知集合M,N⊆I,若M∩N=N,则( )
| A. | ∁IM?∁IN | B. | M⊆∁IN | C. | ∁IM⊆∁IN | D. | M?∁IN |
19.某中学进行高一学生体检,根据检查的学生每分钟脉搏数绘制了频率分布直方图(如图所示),根据频率分布直方图估计每分钟搏数在[69,85]的概率约为0.6.
| 组号 | 分组 | 频数 |
| 1 | [53,61) | 5 |
| 2 | [61,69) | 14 |
| 3 | [69,77) | 25 |
| 4 | [77,85) | 11 |
| 5 | [85,93) | 5 |
19.函数f(x)=cosx+|cosx|,x∈R是( )
| A. | 最小正周期是π | B. | 区间[0,2]上的增函数 | ||
| C. | 图象关于点(kπ,0)(k∈Z)对称 | D. | 周期函数且图象有无数条对称轴 |
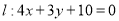 ,半径为
,半径为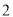 的圆
的圆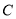 与
与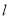 相切,圆心
相切,圆心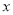 轴上且在直线
轴上且在直线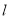 的右上方.
的右上方.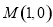 且与圆
且与圆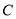 交于
交于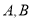 两点(
两点(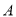 在
在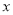 轴上方,B在
轴上方,B在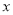 轴正半轴上是否存在定点
轴正半轴上是否存在定点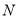 ,使得
,使得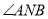 ?若存在,请求出点
?若存在,请求出点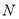 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.