题目内容
m是一条直线,α,β是两个不同的平面,以下命题正确的是( )
| A、若m∥α,α∥β,则m∥β |
| B、若m∥α,m∥β,则α∥β |
| C、若m∥α,α⊥β,则m⊥β |
| D、若m∥α,m⊥β,则α⊥β |
考点:空间中直线与平面之间的位置关系
专题:空间位置关系与距离
分析:由直线与平面的位置关系能判断A的正误;由直线与平面、平面与平面的位置关系能判断B的正误;由直线与平面的位置关系能判断C的正误;由平面与平面垂直的判定定理能判断D的正误.
解答:
解:若m∥α,α∥β,
则m∥β或m?β,故A错误;
若m∥α,m∥β,
则α∥β或α与β相交,故B错误;
若m∥α,α⊥β,
则m?β或m∥β或m与β相交,故C错误;
若m∥α,m⊥β,
则由平面与平面垂直的判定定理知α⊥β,故D正确.
故选:D.
则m∥β或m?β,故A错误;
若m∥α,m∥β,
则α∥β或α与β相交,故B错误;
若m∥α,α⊥β,
则m?β或m∥β或m与β相交,故C错误;
若m∥α,m⊥β,
则由平面与平面垂直的判定定理知α⊥β,故D正确.
故选:D.
点评:本题考查直线与平面、平面与平面的位置关系的判断,是中档题,解题时要注意空间思维能力的培养.

练习册系列答案
相关题目
已知i是虚数单位,则
等于( )
| 3-i |
| 2+i |
| A、-1+i | B、-1-i |
| C、1+i | D、1-i |
如图,在△ABC中,AB=AC=BC=2,则
•
=( )

| AB |
| BC |

| A、1 | B、-1 | C、2 | D、-2 |
若函数f(x)=x+
(b∈R)的导函数在区间(1,2)上有零点,则f(x)在下列区间单调递增的是( )
| b |
| x |
| A、(-2,0) |
| B、(0,1) |
| C、(1,+∞) |
| D、(-∞,-2) |
 在长方体ABCD-A1B1C1D1中,AB=AD=2,AA1=a,E,F分别为AD,CD的中点.
在长方体ABCD-A1B1C1D1中,AB=AD=2,AA1=a,E,F分别为AD,CD的中点.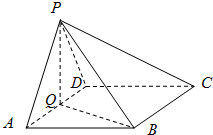 如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的
如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,PA=AB=
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,PA=AB=