题目内容

14．某几何体的三视图如图所示，则其体积为（　　）
A．4B．$4\sqrt{2}$C．$4\sqrt{3}$D．8

分析 几何体为四棱锥，底面为直角梯形，高为侧视图三角形的高．

解答 解：由三视图可知几何体为四棱锥，棱锥底面为俯视图中的直角梯形，棱锥的高为侧视图中等腰三角形的高．
∴四棱锥的高h=$\sqrt{5-1}$=2，
∴棱锥的体积V=$\frac{1}{3}×\frac{1}{2}×（2+4）×2×2$=4．
故选A．

点评 本题考查了棱锥的结构特征，三视图，体积计算，属于基础题．

练习册系列答案
相关题目
4．如图，在矩形ABCD中，AB=2，AD=4，点E在线段AD上且AE=3，现分别沿BE，CE将△ABE，△DCE翻折，使得点D落在线段AE上，则此时二面角D-EC-B的余弦值为（　　）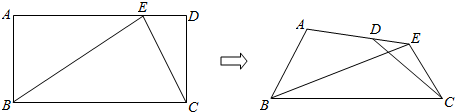
A．$\frac{4}{5}$B．$\frac{5}{6}$C．$\frac{6}{7}$D．$\frac{7}{8}$
5．如图，在△ABC中，AD⊥AB，$\overrightarrow{BC}=2\sqrt{3}\overrightarrow{BD}$，$|{\overrightarrow{AD}}|=1$，则$\overrightarrow{AC}•\overrightarrow{AD}$=（　　）
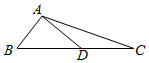
A．$2\sqrt{3}$B．$\sqrt{3}$C．$\frac{{\sqrt{3}}}{2}$D．$\frac{{\sqrt{3}}}{3}$
2．函数y=x2cosx在x=1处的导数是（　　）
A．0B．2cos1-sin1C．cos1-sin1D．1
9．已知直线l：kx-y-2k-1=0（k∈R）．
（1）若直线l过定点P，求点P的坐标；
（2）若直线l交x轴正半轴于点A，交y轴正半轴于点B，O为坐标原点，且|OA|=|OB|，求k的值．
19．两圆x2+y2=9和x2+y2-18x+16y+45=0的公切线有（　　）条．
A．1B．2C．3D．4
6．下列式子中成立的是（　　）
A．log76＜log67B．1.013.4＞1.013.5C．3.50.3＜3.40.3D．log0.44＜log0.46
3．已知点P是圆C：x2+y2-8x-8y+28=0上任意一点，曲线N：x2+4y2=4与x轴交于A，B两点，直线OP与曲线N交于点M，记直线MA，MB，OP的斜率分别为k1，k2，k3，则k1•k2•k3的取值范围是[$-\frac{4+\sqrt{7}}{12}，-\frac{4-\sqrt{7}}{12}$]．
4．函数y=sin2x+2sinxcosx+3cos2x-2，x∈R，下列判断正确的是（　　）
A．最大值为2，周期是πB．最大值为2，周期是2π
C．最大值为$\sqrt{2}$，周期是πD．最大值为$\sqrt{2}$，周期是2π

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网