题目内容
4.如图,在矩形ABCD中,AB=2,AD=4,点E在线段AD上且AE=3,现分别沿BE,CE将△ABE,△DCE翻折,使得点D落在线段AE上,则此时二面角D-EC-B的余弦值为( )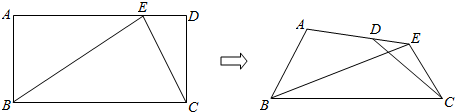
| A. | $\frac{4}{5}$ | B. | $\frac{5}{6}$ | C. | $\frac{6}{7}$ | D. | $\frac{7}{8}$ |
分析 在折叠前的矩形中连接BD交EC于O,得到BD⊥CE,从而得到折起后,∴∠BOD是二面角D-EC-B的平面角,利用余弦定理进行求解即可.
解答 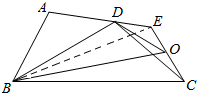
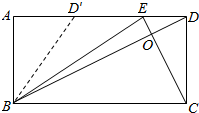 解:在折叠前的矩形中连接BD交EC于O,
解:在折叠前的矩形中连接BD交EC于O,
∵BC=4,CD=2,CD=2,DE=1,
∴$\frac{BC}{CD}=\frac{CD}{DE}$,即△BCD∽△CDE,
∴∠DBC=∠ECD,
∴∠DBC=∠ECD,
∴∠ECD+∠ODC=90°,即BD⊥CE,
折起后,
∵BO⊥CE,DO⊥CE,
∴∠BOD是二面角D-EC-B的平面角,
在△BOD中,OD=$\frac{2\sqrt{5}}{5}$,OB=BD-OD=2$\sqrt{5}$-$\frac{2\sqrt{5}}{5}$=$\frac{8\sqrt{5}}{5}$,
BD=$\sqrt{A{B}^{2}+A{D}^{2}}$=2$\sqrt{2}$,
由余弦定理得cos∠BOD=$\frac{O{D}^{2}+O{B}^{2}-B{D}^{2}}{2OD•DB}$=$\frac{7}{8}$,
故选:D.
点评 本题主要考查二面角的求解,根据折叠前后直线的位置关系以及二面角的平面角的定义作出二面角的平面角是解决本题的关键.综合性较强,难度较大.

练习册系列答案
相关题目
15.已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{25}$=1(a>5)的两个焦点为F1、F2,且|F1F2|=8.弦AB过点F1,则△ABF2的周长为( )
| A. | 10 | B. | 20 | C. | 2$\sqrt{41}$ | D. | 4$\sqrt{41}$ |
14.某几何体的三视图如图所示,则其体积为( )


| A. | 4 | B. | $4\sqrt{2}$ | C. | $4\sqrt{3}$ | D. | 8 |