题目内容
12.已知函数f(x)=sin$\frac{x}{2}$+$\sqrt{3}$cos$\frac{x}{2}$,x∈R.(1)求f(x)取最大值时相应的x的集合;
(2)求函数f(x)的最小正周期和单调递增区间.
分析 由三角函数化简可得$y=sin\frac{x}{2}+\sqrt{3}cos\frac{x}{2}=2sin(\frac{x}{2}+\frac{π}{3})$,
(1)当$\frac{x}{2}+\frac{π}{3}=2kπ+\frac{π}{2}$,即$x=4kπ+\frac{π}{3},k∈Z$时,y取得最大值,可得此时x的集合;
(2)由周期公式可得最小正周期,解$-\frac{π}{2}+2kπ≤\frac{x}{2}+\frac{π}{3}≤\frac{π}{2}+2kπ,k∈Z$可得单调递增区间.
解答 解:由三角函数化简可得$y=sin\frac{x}{2}+\sqrt{3}cos\frac{x}{2}=2sin(\frac{x}{2}+\frac{π}{3})$,
(1)当$\frac{x}{2}+\frac{π}{3}=2kπ+\frac{π}{2}$,即$x=4kπ+\frac{π}{3},k∈Z$时,y取得最大值2,
此时x的集合为$\left\{{x|x=4kπ+\frac{π}{3},k∈Z}\right\}$;
(2)由周期公式可得最小正周期$T=\frac{2π}{{\frac{1}{2}}}=4π$,
解$-\frac{π}{2}+2kπ≤\frac{x}{2}+\frac{π}{3}≤\frac{π}{2}+2kπ,k∈Z$可得$-\frac{5π}{3}+4kπ≤x≤\frac{π}{3}+4kπ,k∈Z$;
∴函数f(x)的单调增区间为:$[-\frac{5π}{3}+4kπ,\frac{π}{3}+4kπ],k∈Z$.
点评 本题考查三角函数恒等变换,涉及三角函数的周期性和最值,属基础题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
2.若直线x=a是函数y=sin(x+$\frac{π}{6}$)图象的一条对称轴,则a的值可以是( )
| A. | $\frac{π}{3}$ | B. | $\frac{π}{2}$ | C. | -$\frac{π}{6}$ | D. | -$\frac{π}{3}$ |
1.已知集合M={x|x2-1≤0},N={x|-2<x<1,x∈Z},则M∩N( )
| A. | {-1,0} | B. | {1} | C. | {-1,0,1} | D. | ∅ |
2.已知函数g(x)=lnx-mx2-nx(m,n∈R)在x=2处取得最大值,则m的取值范围为( )
| A. | (-$\frac{1}{8}$,0)∪(0,+∞) | B. | (-$\frac{1}{8}$,+∞) | C. | (-∞,0)∪(0,$\frac{1}{8}$) | D. | (0,+∞) |
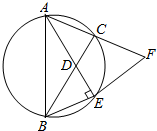 如图,在△ABC中,∠BAC的平分线交BC于D,交△ABC的外接圆于E,延长AC到F,使得AC•AF=AD•AE,连按EF.
如图,在△ABC中,∠BAC的平分线交BC于D,交△ABC的外接圆于E,延长AC到F,使得AC•AF=AD•AE,连按EF.