题目内容
2.已知函数g(x)=lnx-mx2-nx(m,n∈R)在x=2处取得最大值,则m的取值范围为( )| A. | (-$\frac{1}{8}$,0)∪(0,+∞) | B. | (-$\frac{1}{8}$,+∞) | C. | (-∞,0)∪(0,$\frac{1}{8}$) | D. | (0,+∞) |
分析 求出g(x)的导数,由g(x)在x=2处取得最大值,也为极大值,即有g′(2)=0,即n=$\frac{1}{2}$-4m,运用韦达定理求得1-2mx2-nx=0的另一个根,讨论m的范围,即可得到所求范围.
解答 解:函数g(x)=lnx-mx2-nx的导数为g′(x)=$\frac{1}{x}$-2mx-n,
由g(x)在x=2处取得最大值,也为极大值,
即有g′(2)=0,即n=$\frac{1}{2}$-4m,
由1-2mx2-nx=0的一个根为2,
由韦达定理可得另一个根为-$\frac{1}{4m}$,
当m>0时,-$\frac{1}{4m}$<0,g′(x)=0的根为2,
即有x=2取得极大值,也为最大值;
当m<0时,-$\frac{1}{4m}$>2,解得-$\frac{1}{8}$<m<0,g(x)存在极大值和极小值,
x=2为最大值点.
当m=0时,g′(x)=$\frac{1}{x}$-$\frac{1}{2}$,可得g(x)在x=2处取得最大值,也为极大值.
综上可得m的范围为m>-$\frac{1}{8}$.
故选B.
点评 本题考查导数的运用:求单调区间和极值、最值,注意运用函数在某个区间只有一个极值,即为最值的结论是解题的关键.

练习册系列答案
相关题目
14.为调查当前干部的作风情况,某市检察机关从该市干部名单库中随机抽取100名干部,通过问卷调查,实际考核等方式,对每个干部依次考核成绩,分A,B,C,D,E五个等级进行测评,最后对数据做如下统计:
(1)根据上级要求,对考核测评为E级的干部,将从干部名单库中清除;对考核测评为D级的干部,要求进行教育整改;而对考核测评为A级的干部,将授予“人民楷模”的称号,现从该市干部中,随机抽取3人,求这三人来自不同的考核测评等级,且都不是被清除人的概率(精确到小数点后三位);
(2)若从该市干部中,随机抽取5人,求抽取的是“人民楷模”的人数ξ的数学期望.
| 成绩 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100) | 合计 |
| 等级 | E | D | C | B | A | |
| 频数 | 2 | 24 | 36 | 30 | 8 | 100 |
| 频率 | 0.02 | 0.24 | 0.36 | 0.3 | 0.08 | 1 |
(2)若从该市干部中,随机抽取5人,求抽取的是“人民楷模”的人数ξ的数学期望.
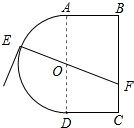 一个玩具盘由一个直径为2米的半圆O和一个矩形ABCD构成,AB=1米,如图所示,小球从A点出发以大小为5v的速度沿半圆O轨道滚到某点E处,经弹射器以6v的速度沿与点E切线垂直的方向弹射到落袋区BC内,落点记为F,设∠AOE=θ弧度,小球从A到F所需时间为T.
一个玩具盘由一个直径为2米的半圆O和一个矩形ABCD构成,AB=1米,如图所示,小球从A点出发以大小为5v的速度沿半圆O轨道滚到某点E处,经弹射器以6v的速度沿与点E切线垂直的方向弹射到落袋区BC内,落点记为F,设∠AOE=θ弧度,小球从A到F所需时间为T.