题目内容
9.某校为研究学生语言学科的学习情况,现对高二200名学生英语和语文某次考试成绩进行抽样分析.将200名学生编号为001,002,…,200,采用系统抽样的方法等距抽取10名学生,将10名学生的两科成绩(单位:分)绘成折线图如下:
(Ⅰ)若第一段抽取的学生编号是006,写出第五段抽取的学生编号;
(Ⅱ)在这两科成绩差超过20分的学生中随机抽取2人进行访谈,求2人成绩均是语文成绩高于英语成绩的概率;
(Ⅲ)根据折线图,比较该校高二年级学生的语文和英语两科成绩,写出你的结论和理由.
分析 (Ⅰ)第一段抽取的学生编号是006,间隔为20,即可写出第五段抽取的学生编号;
(Ⅱ)确定基本事件的个数,可得结论;
(Ⅲ)根据折线图,可以估计该校高二年级学生的语文成绩平均分高,语文成绩相对更稳定.
解答 解:(Ⅰ)第一段抽取的学生编号是006,间隔为20,第五段抽取的学生编号为086;
(Ⅱ)这两科成绩差超过20分的学生,共5人,语文成绩高于英语成绩,有3人,从中随机抽取2人进行访谈,有${C}_{5}^{2}$=10种,2人成绩均是语文成绩高于英语成绩,有3种,故2人成绩均是语文成绩高于英语成绩的概率是$\frac{3}{10}$;
(Ⅲ)根据折线图,可以估计该校高二年级学生的语文成绩平均分高,语文成绩相对更稳定.
点评 本题考查系统抽样,考查概率的计算,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
19.若命题“?x0∈R,x02+(a-1)x0+1<0”是真命题,则实数a的取值范围是( )
| A. | [-1,3] | B. | (-1,3) | C. | (-∞,-1]∪[3,+∞) | D. | (-∞,-1)∪(3,+∞) |
17.某市对大学生毕业后自主创业人员给予小额贷款补贴,贷款期限分为6个月、12个月、18个月、24个月、36个月五种,对于这五种期限的贷款政府分别补贴200元、300元、300元、400元、400元,从2016年享受此项政策的自主创业人员中抽取了100人进行调查统计,选取贷款期限的频数如表:
(Ⅰ)若小王准备申请此项贷款,求其获得政府补贴不超过300元的概率(以上表中各项贷款期限的频率作为2017年自主创业人员选择各种贷款期限的概率);
(Ⅱ)若小王和小李同时申请此项贷款,求两人所获得政府补贴之和不超过600元的概率.
| 贷款期限 | 6个月 | 12个月 | 18个月 | 24个月 | 36个月 |
| 频数 | 20 | 40 | 20 | 10 | 10 |
(Ⅱ)若小王和小李同时申请此项贷款,求两人所获得政府补贴之和不超过600元的概率.
4.S(A)表示集合A中所有元素的和,且A⊆{1,2,3,4,5},若S(A)能被3整除,则符合条件的非空集合A的个数是( )
| A. | 10 | B. | 11 | C. | 12 | D. | 13 |
14.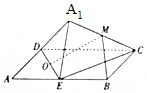 如图,矩形ABCD中,AB=2AD,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE(A1∉平面ABCD),若M、O分别为线段A1C、DE的中点,则在△ADE翻转过程中,下列说法错误的是( )
如图,矩形ABCD中,AB=2AD,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE(A1∉平面ABCD),若M、O分别为线段A1C、DE的中点,则在△ADE翻转过程中,下列说法错误的是( )
 如图,矩形ABCD中,AB=2AD,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE(A1∉平面ABCD),若M、O分别为线段A1C、DE的中点,则在△ADE翻转过程中,下列说法错误的是( )
如图,矩形ABCD中,AB=2AD,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE(A1∉平面ABCD),若M、O分别为线段A1C、DE的中点,则在△ADE翻转过程中,下列说法错误的是( )| A. | 与平面A1DE垂直的直线必与直线BM垂直 | |
| B. | 异面直线BM与A1E所成角是定值 | |
| C. | 一定存在某个位置,使DE⊥MO | |
| D. | 三棱锥A1-ADE外接球半径与棱AD的长之比为定值 |
1.已知集合A={y|0≤y<2,y∈N},B={x|x2-4x-5≤0,x∈N},则A∩B=( )
| A. | {1} | B. | {0,1} | C. | [0,2) | D. | ∅ |
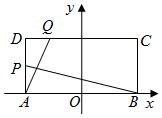 如图,在矩形ABCD中,|AB|=4,|AD|=2,O为AB中点,P,Q分别是AD和CD上的点,且满足①$\frac{|AP|}{|AD|}$=$\frac{|DQ|}{|DC|}$,②直线AQ与BP的交点在椭圆E:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)上.
如图,在矩形ABCD中,|AB|=4,|AD|=2,O为AB中点,P,Q分别是AD和CD上的点,且满足①$\frac{|AP|}{|AD|}$=$\frac{|DQ|}{|DC|}$,②直线AQ与BP的交点在椭圆E:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)上.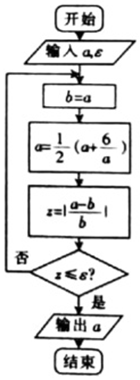 十七世纪英国著名数学家、物理学家牛顿创立的求方程近似解的牛顿迭代法,相较于二分法更具优势,如图给出的是利用牛顿迭代法求方程x2=6的正的近似解的程序框图,若输入a=2,?=0.02,则输出的结果为( )
十七世纪英国著名数学家、物理学家牛顿创立的求方程近似解的牛顿迭代法,相较于二分法更具优势,如图给出的是利用牛顿迭代法求方程x2=6的正的近似解的程序框图,若输入a=2,?=0.02,则输出的结果为( ) 从某市的中学生中随机调查了部分男生,获得了他们的身高数据,整理得到如下频率分布直方图.
从某市的中学生中随机调查了部分男生,获得了他们的身高数据,整理得到如下频率分布直方图.