题目内容
5．若集合A={x|y=lgx}，B={x|y=$\sqrt{1-x}$}，则A∩B等于（ ）| A． | [0，1] | B． | （0，1] | C． | [1，+∞） | D． | （-∞，1] |
分析 求出A中x的范围确定出A，求出B中x的范围确定出B，求出两集合的交集即可．
解答 解：由A中y=lgx，得到x＞0，即A=（0，+∞），
由B中y=$\sqrt{1-x}$，得到1-x≥0，即x≤1，
∴B=（-∞，1]，
则A∩B=（0，1]，
故选：B．
点评 此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．
练习册系列答案
相关题目
如图，在正三棱柱A1B1C1-ABC中，AB=2，A1A=2$\sqrt{3}$，D，F分别是棱AB，AA1的中点，E为棱AC上的动点，则△DEF周长的最小值为$\sqrt{7}$+2．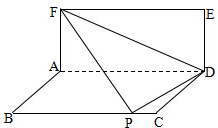
已知两矩形ABCD与ADEF所在的平面互相垂直，AB=1，若将△DEF沿直线FD翻折，使得点E落在边BC上（即点P），则当AD取最小值时，边AF的长是$\sqrt{2}$；此时四面体F-ADP的外接球的半径是$\frac{\sqrt{6}}{2}$．
10．已知A，B为抛物线y2=2px（p＞0）上的两动点，F为其焦点，且满足∠AFB=60°，过弦AB的中点M作抛物线准线的垂线，垂足为N，|MN|=λ|AB|，则λ的最大值为（ ）
| A． | 1 | B． | $\frac{2\sqrt{3}}{3}$ | C． | $\frac{\sqrt{3}}{3}$ | D． | 2 |
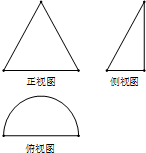某几何体的三视图如图所示，其中正视图是腰长为2cm的等腰三角形，俯视图是半径为1cm的半圆，则该几何体的表面积是$\frac{3π}{2}$+$\sqrt{3}$cm2，体积是$\frac{\sqrt{3}}{6}$πcm3．