题目内容
3. 如图,在正三棱柱A1B1C1-ABC中,AB=2,A1A=2$\sqrt{3}$,D,F分别是棱AB,AA1的中点,E为棱AC上的动点,则△DEF周长的最小值为$\sqrt{7}$+2.
如图,在正三棱柱A1B1C1-ABC中,AB=2,A1A=2$\sqrt{3}$,D,F分别是棱AB,AA1的中点,E为棱AC上的动点,则△DEF周长的最小值为$\sqrt{7}$+2.
分析 由正三棱柱A1B1C1-ABC的性质可得:AA1⊥AB,AA1⊥AC.在Rt△ADF中,利用勾股定理可得DF=2.因此只要求出DE+EF的最小值即可得出.把底面ABC展开与侧面ACC1A1在同一个平面,如图所示,只有当三点D,E,F在同一条直线时,DE+EF取得最小值.利用余弦定理即可得出.
解答 解:由正三棱柱A1B1C1-ABC,可得AA1⊥底面ABC,∴AA1⊥AB,AA1⊥AC.
在Rt△ADF中,DF=$\sqrt{(\sqrt{3})^{2}+{1}^{2}}$=2.
把底面ABC展开与侧面ACC1A1在同一个平面,如图所示,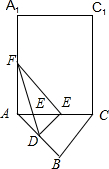
只有当三点D,E,F在同一条直线时,DE+EF取得最小值.
在△ADE中,∠DAE=60°+90°=150°,由余弦定理可得:
DE=$\sqrt{(\sqrt{3})^{2}+{1}^{2}-2\sqrt{3}×cos15{0}^{°}}$=$\sqrt{7}$.
∴△DEF周长的最小值=$\sqrt{7}$+2.
故答案为:$\sqrt{7}$+2.
点评 本题考查了空间几何位置关系、余弦定理、侧面展开图,考查了转化能力、数形结合能力、推理能力与计算能力,属于难题.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案
相关题目
14.复数$\frac{{\sqrt{2}•{i^{2015}}}}{{1-\sqrt{2}i}}$=( )
| A. | $\frac{2}{3}$-$\frac{{\sqrt{2}}}{3}$i | B. | -$\frac{2}{3}$-$\frac{\sqrt{2}}{3}$i | C. | $\frac{2}{3}$+$\frac{\sqrt{2}}{3}$i | D. | -$\frac{2}{3}$+$\frac{\sqrt{2}}{3}$i |
8.在递减数列{an}中,an=-2n2+λn,求实数λ的取值范围是( )
| A. | (-∞,2) | B. | (-∞,3) | C. | (-∞,4) | D. | (-∞,6) |
15.函数f(x)=tan(2x+φ)(-$\frac{π}{2}$<φ<$\frac{π}{2}$)的一个对称中心为($\frac{π}{3}$,0),则φ的值是( )
| A. | -$\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | -$\frac{π}{3}$ | D. | -$\frac{π}{6}$或$\frac{π}{3}$ |
12.已知二次函数f(x)=2x2+1,过点(1,0)做直线l1,l2与f(x)的图象相切于A,B两点,则直线AB的方程为( )
| A. | $\sqrt{6}$x-y+2=0 | B. | x-$\sqrt{6}$y+1=0 | C. | 4x-y+2=0 | D. | x-4y+1=0 |
5.若集合A={x|y=lgx},B={x|y=$\sqrt{1-x}$},则A∩B等于( )
| A. | [0,1] | B. | (0,1] | C. | [1,+∞) | D. | (-∞,1] |
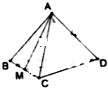 在四面体A-BCD中,棱长为4,M是BC的中点,点P在线段AM上运动,(点P不与A,M重合),过点P做直线l⊥平面ABC,l与平面BCD交于点Q.给出下列命题,其中正确的是①②
在四面体A-BCD中,棱长为4,M是BC的中点,点P在线段AM上运动,(点P不与A,M重合),过点P做直线l⊥平面ABC,l与平面BCD交于点Q.给出下列命题,其中正确的是①②