题目内容
13.四棱锥P-ABCD内接于球,底面ABCD为正方形,PA⊥平面ABCD,PA=AB=2,则此球的表面积为12π.分析 可以将四棱锥P-ABCD补成球的内接长方体,其对角线PC即为球的直径,利用勾股定理,求出球的半径,即可求球的表面积.
解答 解:可以将四棱锥P-ABCD补成球的内接长方体,其对角线PC即为球的直径.
∵PA=AB=2,
∴PC=2$\sqrt{3}$,
∴球的半径为$\sqrt{3}$,
∴球的表面积为4π×3=12π.
故答案为:12π.
点评 本题主要考查球的表面积公式,构造长方体是解决本题的关键.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
12.已知二次函数f(x)=2x2+1,过点(1,0)做直线l1,l2与f(x)的图象相切于A,B两点,则直线AB的方程为( )
| A. | $\sqrt{6}$x-y+2=0 | B. | x-$\sqrt{6}$y+1=0 | C. | 4x-y+2=0 | D. | x-4y+1=0 |
1.已知A(xA,yA)是单位圆上(圆心在坐标原点O)任意一点,且射线OA绕O点逆时针旋转30°到OB交单位圆于点B(xB,yB),则xA-yB的最大值为( )
| A. | $\sqrt{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | 1 | D. | $\frac{1}{2}$ |
8.(x2-x+ay)7的展开式中,x7y2的系数为-$\frac{105}{2}$,则a等于( )
| A. | -2 | B. | $\frac{1}{2}$ | C. | ±2 | D. | ±$\frac{1}{2}$ |
18.已知点A(2,3)、B (-5,2),若直线l过点P (-1,6),且与线段AB相交,则直线l斜率的取值范围是( )
| A. | [-1,1] | B. | (-∞,-1]∪[1,+∞) | C. | (-1,1) | D. | (-∞,-1)∪(1,+∞) |
5.若集合A={x|y=lgx},B={x|y=$\sqrt{1-x}$},则A∩B等于( )
| A. | [0,1] | B. | (0,1] | C. | [1,+∞) | D. | (-∞,1] |
2.下列命题中是假命题的是( )
| A. | ?x∈(0,$\frac{π}{2}$),x>sinx | B. | ?x0∈R,sinx0+cosx0=2 | ||
| C. | “?x∈R,3x>0” | D. | ?x0∈R,x0+$\frac{1}{x_0}$=-3 |
3.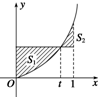 在区间[0,1]上给定曲线y=x2,如图所示,0<t<1,S1,S2是t的函数,则函数g(t)=S1+S2的单调递增区间为( )
在区间[0,1]上给定曲线y=x2,如图所示,0<t<1,S1,S2是t的函数,则函数g(t)=S1+S2的单调递增区间为( )
 在区间[0,1]上给定曲线y=x2,如图所示,0<t<1,S1,S2是t的函数,则函数g(t)=S1+S2的单调递增区间为( )
在区间[0,1]上给定曲线y=x2,如图所示,0<t<1,S1,S2是t的函数,则函数g(t)=S1+S2的单调递增区间为( )| A. | ($\frac{1}{2}$,1) | B. | ($\frac{1}{2}$,2] | C. | [0,1] | D. | (1,2] |
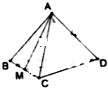 在四面体A-BCD中,棱长为4,M是BC的中点,点P在线段AM上运动,(点P不与A,M重合),过点P做直线l⊥平面ABC,l与平面BCD交于点Q.给出下列命题,其中正确的是①②
在四面体A-BCD中,棱长为4,M是BC的中点,点P在线段AM上运动,(点P不与A,M重合),过点P做直线l⊥平面ABC,l与平面BCD交于点Q.给出下列命题,其中正确的是①②