题目内容
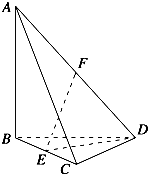 如图,四面体ABCD中,AB、BC、BD两两垂直,AB=BC=BD=4,E、F分别为棱BC、AD的中点.
如图,四面体ABCD中,AB、BC、BD两两垂直,AB=BC=BD=4,E、F分别为棱BC、AD的中点.(1)求异面直线AB与EF所成角的余弦值;
(2)求E到平面ACD的距离;
(3)求EF与平面ACD所成角的正弦值.
考点:直线与平面所成的角,异面直线及其所成的角,点、线、面间的距离计算
专题:空间位置关系与距离,空间角
分析:(1)如图,分别以直线BC,BD,AB为x,y,z轴建立空间直角坐标系,求出异面直线AB与EF的方向向量,代入向量夹角公式,可得异面直线AB与EF所成角的余弦值;
(2)求出平面ACD的一个法向量
=(1,1,1),结合F∈平面ACD,
=(-2,2,2),可得:E到平面ACD的距离d=
;
(3)由(2)中平面ACD的一个法向量
=(1,1,1),设EF与平面ACD所成角为α.则sinα=cos<
,
>.
(2)求出平面ACD的一个法向量
| n |
| EF |
|
| ||||
|
|
(3)由(2)中平面ACD的一个法向量
| n |
| n |
| EF |
解答:
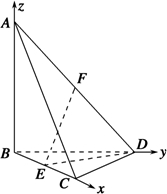 解:(1)如图,分别以直线BC,BD,AB为x,y,z轴建立空间直角坐标系,
解:(1)如图,分别以直线BC,BD,AB为x,y,z轴建立空间直角坐标系,
∵AB=BC=BD=4,E、F分别为棱BC、AD的中点.
∴A(0,0,4),C(4,0,0),D(0,4,0),E(2,0,0),F(0,2,2),
∵
=(0,0,-4),
=(-2,2,2),
设异面直线AB与EF所成角为θ,
则cosθ=
=
=
,
即异面直线AB与EF所成角的余弦值为
;
(2)设平面ACD的一个法向量
=(x,y,1),
∵
=(4,0,-4),
=(-4,4,0),
由
,得
,
故
=(1,1,1),
∵F∈平面ACD,
=(-2,2,2),
∴E到平面ACD的距离d=
=
=
;
(3)由(2)中平面ACD的一个法向量
=(1,1,1),
设EF与平面ACD所成角为α.
则sinα=cos<
,
>=
=
=
.
 解:(1)如图,分别以直线BC,BD,AB为x,y,z轴建立空间直角坐标系,
解:(1)如图,分别以直线BC,BD,AB为x,y,z轴建立空间直角坐标系,∵AB=BC=BD=4,E、F分别为棱BC、AD的中点.
∴A(0,0,4),C(4,0,0),D(0,4,0),E(2,0,0),F(0,2,2),
∵
| AB |
| EF |
设异面直线AB与EF所成角为θ,
则cosθ=
|
| ||||
|
|
| 8 | ||
4×2
|
| ||
| 3 |
即异面直线AB与EF所成角的余弦值为
| ||
| 3 |
(2)设平面ACD的一个法向量
| n |
∵
| AC |
| CD |
由
|
|
故
| n |
∵F∈平面ACD,
| EF |
∴E到平面ACD的距离d=
|
| ||||
|
|
| 2 | ||
|
2
| ||
| 3 |
(3)由(2)中平面ACD的一个法向量
| n |
设EF与平面ACD所成角为α.
则sinα=cos<
| n |
| EF |
|
| ||||
|
|
| 2 | ||||
|
| 1 |
| 3 |
点评:本题考查的知识点是直线与平面所成的角,异面直线及其所成的角,点到平面的距离,建立空间坐标系,将空间夹角问题和距离问题转化为向量夹角和向量射影问题是解答的关键.

练习册系列答案
相关题目
定义在R上的函数f(x),存在无数个实数x满足f(x+2)=f(x),则f(x)( )
| A、是周期为1的周期函数 |
| B、是周期为2的周期函数 |
| C、是周期为4的周期函数 |
| D、不一定是周期函数 |
在平行四边形ABCD中,AB=4,AD=2,E,F分别是BC,CD的中点,且
•
=-15,则∠ABC=( )
| DE |
| BF |
A、
| ||
B、
| ||
C、
| ||
D、
|
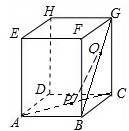 如图,正方体ABCD-EFGH的棱长为a,点P在AC上,点Q在BG上,AP=BQ=a,求证:PQ⊥AD.
如图,正方体ABCD-EFGH的棱长为a,点P在AC上,点Q在BG上,AP=BQ=a,求证:PQ⊥AD.