题目内容
20.若x,y满足x2-2xy+3y2=4,则$\frac{1}{{x}^{2}+{y}^{2}}$的最大值与最小值的和是1.分析 设x=rcosα,y=rsinα,(r>0);从而可得r2(cos2α-2cosαsinα+3sin2α)=4,而$\frac{1}{{x}^{2}+{y}^{2}}$=$\frac{1}{{r}^{2}}$,从而化简即可.
解答 解:设x=rcosα,y=rsinα,(r>0);
∵x2-2xy+3y2=4,
∴r2cos2α-2rcosαrsinα+3r2sin2α=4,
∴r2(cos2α-2cosαsinα+3sin2α)=4,
∴$\frac{1}{{x}^{2}+{y}^{2}}$=$\frac{1}{{r}^{2}}$
=$\frac{1}{4}$(cos2α-2cosαsinα+3sin2α)
=$\frac{1}{4}$(1-sin2α+2sin2α)
=$\frac{1}{4}$(1-sin2α+1-cos2α)
=$\frac{1}{4}$(2-$\sqrt{2}$sin(2α+$\frac{π}{4}$)),
故当sin(2α+$\frac{π}{4}$)=1时,$\frac{1}{{x}^{2}+{y}^{2}}$有最小值$\frac{1}{4}$(2-$\sqrt{2}$);
当sin(2α+$\frac{π}{4}$)=-1时,$\frac{1}{{x}^{2}+{y}^{2}}$有最大值$\frac{1}{4}$(2+$\sqrt{2}$);
而$\frac{1}{4}$(2-$\sqrt{2}$)+$\frac{1}{4}$(2+$\sqrt{2}$)=1,
故答案为:1.
点评 本题考查了方程思想的应用及整体思想与转化思想的应用,同时考查了换元法的应用.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
5.已知函数f(x)=mex+x2+nx,{x|f(x)=0}={x|f(f(x))=0}≠∅,则m+n的取值范围为( )
| A. | (0,4) | B. | [0,4) | C. | [0,4] | D. | (4,+∞) |
2.已知函数f(x)=2sin(ωx+$\frac{π}{3}$)(ω>0)的图象与函数g(x)=cos(2x+φ)(|φ|<$\frac{π}{2}$)的图象的对称中心完全相同,则φ=( )
| A. | $\frac{π}{6}$ | B. | -$\frac{π}{6}$ | C. | $\frac{π}{3}$ | D. | -$\frac{π}{3}$ |
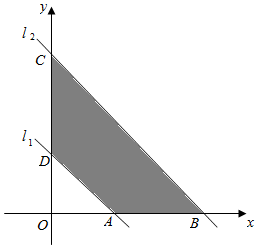 如图,已知直线l1:x+y-1=0,现将直线l1向上平移到直线l2的位置,若l2、l1和坐标轴围成的梯形面积为4,求l2的方程.
如图,已知直线l1:x+y-1=0,现将直线l1向上平移到直线l2的位置,若l2、l1和坐标轴围成的梯形面积为4,求l2的方程.