题目内容
3.在平面直角坐标系xOy中,已知射线OA:x-y=0(x≥0),OB:x+2y=0(x≥0),过点P(1,0)作直线分别交射线OA,OB于点A,B,AB的中点为P.(1)求直线AB的方程;
(2)过点C(6,-1)作直线l,使得A,B两点到直线l的距离相等,求直线l的方程.
分析 (1)根据A在射线OA上,设A(a,a),根据P为线段AB中点,利用中点坐标公式变形出B坐标,代入射线OB解析式求出a的值,确定出A与B坐标,即可求出直线AB解析式.
(2)当AB∥直线l时,用点斜式求得直线l的方程;直线l经过线段AB的中点P(1,0),则由两点式求得直线l(即直线CP)的方程,综合可得结论.
解答 解:(1)∵已知射线OA:x-y=0(x≥0),OB:x+2y=0(x≥0),
过点P(1,0)作直线分别交射线OA,OB于点A,B,AB的中点为P.
设A(a,a),∵A、B的中点为P,∴B(2-a,-a),
将B代入射线OB解析式得:(2-a)+2×(-a)=0,
解得:a=$\frac{2}{3}$,∴A($\frac{2}{3}$,$\frac{2}{3}$),B($\frac{4}{3}$,-$\frac{2}{3}$),P(1,0)
则直线AB为:$\frac{y+\frac{2}{3}}{\frac{2}{3}+\frac{2}{3}}$=$\frac{x-\frac{4}{3}}{\frac{2}{3}-\frac{4}{3}}$,即2x+y-2=0.
(2)过点C(6,-1)作直线l,使得A,B两点到直线l的距离相等,
若AB∥直线l,则直线l的斜率为KAB =-2,
故直线l的方程为y+1=-2(x-6),即 2x+y-11=0.
若直线l经过线段AB的中点P(1,0),则由两点式求得直线l(即直线CD)的方程为$\frac{y-0}{-1-0}$=$\frac{x-1}{6-1}$,
即 x+5y-1=0.
综上可得,要求的直线l的方程为2x+y-11=0 或x+5y-1=0.
点评 此题考查了点到直线的距离公式,线段中点坐标公式,以及两直线的交点坐标,用点斜式和两点式求直线的方程,属于基础题.

 53天天练系列答案
53天天练系列答案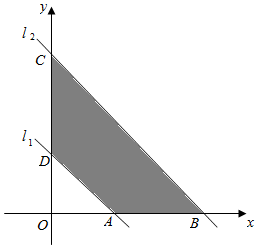 如图,已知直线l1:x+y-1=0,现将直线l1向上平移到直线l2的位置,若l2、l1和坐标轴围成的梯形面积为4,求l2的方程.
如图,已知直线l1:x+y-1=0,现将直线l1向上平移到直线l2的位置,若l2、l1和坐标轴围成的梯形面积为4,求l2的方程.