题目内容
2.已知a,b为空间两条不重合的直线,α,β为空间两个不重合的平面,则以下结论正确的是( )| A. | 若α⊥β,a?α,则a⊥β | B. | 若α⊥β,a⊥β,则a∥α | C. | 若a?α,a∥β,则α∥β | D. | 若a?α,a⊥β,则α⊥β |
分析 利用线面、平面与平面平行、垂直的判定与性质,即可得出结论.
解答 解:对于A,若α⊥β,a?α,则:a⊥β或a与β相交或a?β,不正确;
对于B,因为一条直线与一个平面都垂直于同一个平面,此面与线的位置关系是线在面内或线与面平行,不正确;
对于C,根据平面与平面平行的判定定理,可知不正确;
对于D,根据平面与平面垂直的判定定理,可知正确.
故选:D.
点评 本题考查空间中直线与平面之间的位置关系,解题的关键是有着较高的空间想像能力以及对空间中线面位置关系的了解,本题考查了空间想像能力及打理判断的能力,是考查基本概念的常见题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
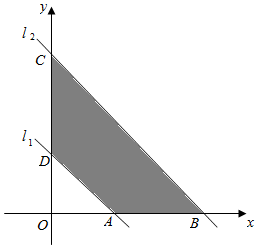 如图,已知直线l1:x+y-1=0,现将直线l1向上平移到直线l2的位置,若l2、l1和坐标轴围成的梯形面积为4,求l2的方程.
如图,已知直线l1:x+y-1=0,现将直线l1向上平移到直线l2的位置,若l2、l1和坐标轴围成的梯形面积为4,求l2的方程.