题目内容
11.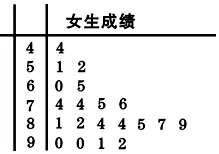 为了研究某学科成绩(满分100分)是否与学生性别有关,采用分层抽样的方法,从高二年级抽取了30名男生和20名女生的该学科成绩,得到如图所示女生成绩的茎叶图.其中抽取的男生中有21人的成绩在80分以下,规定80分以上为优秀(含80分).
为了研究某学科成绩(满分100分)是否与学生性别有关,采用分层抽样的方法,从高二年级抽取了30名男生和20名女生的该学科成绩,得到如图所示女生成绩的茎叶图.其中抽取的男生中有21人的成绩在80分以下,规定80分以上为优秀(含80分).(1)请根据题意,将2×2列联表补充完整;
| 优秀 | 非优秀 | 总计 | |
| 男生 | |||
| 女生 | |||
| 总计 | 50 |
附:x2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
| 参考数据 | 当x2≤2.706时,无充分证据判定变量A,B有关联,可以认为两变量无关联; |
| 当x2>2.706时,有90%的把握判定变量A,B有关联; | |
| 当x2>3.841时,有95%的把握判定变量A,B有关联; | |
| 当x2>6.635时,有99%的把握判定变量A,B有关联. |
分析 (1)根据图示,将2×2列联表补充完整,
(2)根据列联表计算X2,对照临界值即可得出正确的结论.
解答 解:(1)根据图示,将2×2列联表补充完整如下:
| 优秀 | 非优秀 | 总计 | |
| 男生 | 9 | 21 | 30 |
| 女生 | 11 | 9 | 20 |
| 总计 | 20 | 30 | 50 |
(2)根据列联表可以求得X2=$\frac{50{×(9×9-11×21)}^{2}}{20×30×20×30}$≈3.125>2.706;
(式子列对结果不对得5分) …(14分)
因此有90%的把握认为该学科成绩与性别有关.…(17分)
点评 本题考查了列联表与独立性检验的应用问题,是基础题.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
2.若复数(1-i)(a+i)在复平面内对应的点在第二象限,则实数a的取值范围是( )
| A. | (-∞,1) | B. | (-∞,-1) | C. | (1,+∞) | D. | (-1,+∞) |
3.下列说法中错误的是( )
| A. | 总体中的个体数不多时宜用简单随机抽样 | |
| B. | 系统抽样过程中,在总体均分后的每一部分中抽取一个个体,得到所需样本 | |
| C. | 百货商场的抓奖活动是抽签法 | |
| D. | 整个抽样过程中,每个个体被抽取的概率相等(有剔除时例外) |
1.海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了100个网箱,测量各箱水产品的产量(单位:kg),其频率分布直方图如下:
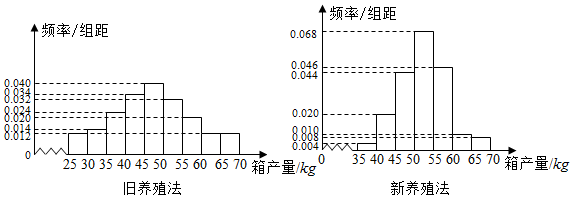
(1)记A表示事件“旧养殖法的箱产量低于50kg”,估计A的概率;
(2)填写下面列联表,并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关:
(3)根据箱产量的频率分布直方图,对两种养殖方法的优劣进行比较.
附:
K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$.

(1)记A表示事件“旧养殖法的箱产量低于50kg”,估计A的概率;
(2)填写下面列联表,并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关:
| 箱产量<50kg | 箱产量≥50kg | |
| 旧养殖法 | ||
| 新养殖法 |
附:
| P(K2≥K) | 0.050 | 0.010 | 0.001 |
| K | 3.841 | 6.635 | 10.828 |
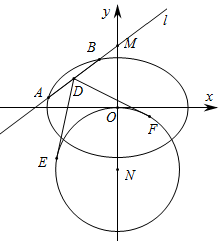 在平面直角坐标系xOy中,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,椭圆C截直线y=1所得线段的长度为2$\sqrt{2}$.
在平面直角坐标系xOy中,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,椭圆C截直线y=1所得线段的长度为2$\sqrt{2}$.