题目内容
已知α,β均为锐角,且sinα=
,cosβ=
,
(1)求sin(α-β)的值
(2)求α-β
| 1 | ||
|
| 1 | ||
|
(1)求sin(α-β)的值
(2)求α-β
考点:两角和与差的正弦函数
专题:三角函数的求值
分析:(1)利用同角三角函数基本关系分别求得cosα和sinβ的值,利用两角和公式求得sin(α-β)的值.
(2)根据)α,β的范围判断出α-β的范围,最后根据sin(α-β)的值求得答案.
(2)根据)α,β的范围判断出α-β的范围,最后根据sin(α-β)的值求得答案.
解答:
解:(1)∵α,β均为锐角,
∴cosα=
=
,sinβ=
=
,
∴sin(α-β)=sinαcosβ-cosαsinβ=
×
-
×
=-
,
(2)∵α,β均为锐角,
∴-
<α-β<
,
∵sin(α-β)=-
,
∴α-β=-
∴cosα=
1-
|
2
| ||
| 5 |
1-
|
3
| ||
| 10 |
∴sin(α-β)=sinαcosβ-cosαsinβ=
| 1 | ||
|
| 1 | ||
|
| 2 | ||
|
| 3 | ||
|
| ||
| 2 |
(2)∵α,β均为锐角,
∴-
| π |
| 2 |
| π |
| 2 |
∵sin(α-β)=-
| ||
| 2 |
∴α-β=-
| π |
| 4 |
点评:本题主要考查了两角和与差的正弦函数.考查了学生基础知识的运用和运算能力.

练习册系列答案
相关题目
设m,n是两条不同的直线,α,β是两个不同的平面,则下列命题中的真命题是( )
| A、若m⊥β,m∥α,则α⊥β |
| B、若m?β,α⊥β,则m⊥α |
| C、若m∥α,n∥β,α∥β,则m∥n |
| D、若m?α,n?β,m∥n,则α∥β |
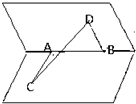 二面角的棱上有A、B两点,直线AC、BD分别在这个二面角的量两个半平面内,且都垂直于AB.已知AB=4,AC=6,BD=8,CD=2
二面角的棱上有A、B两点,直线AC、BD分别在这个二面角的量两个半平面内,且都垂直于AB.已知AB=4,AC=6,BD=8,CD=2