题目内容
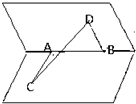二面角的棱上有A、B两点，直线AC、BD分别在这个二面角的量两个半平面内，且都垂直于AB．已知AB=4，AC=6，BD=8，CD=2| 17 |
考点：二面角的平面角及求法
专题：计算题,空间角
分析：将向量
转化成
=
+
+
，然后等式两边同时平方表示出向量
的模，再根据向量的数量积求出向量
，
的夹角，即可求出二面角的大小．
| CD |
| CD |
| CA |
| AB |
| BD |
| CD |
| CA |
| BD |
解答：
解：由条件，知
•
=0，
•
=0，
=
+
+
．
∴|
|2=62+42+82+2×6×8cos＜
，
＞=（2
）2，
∴cos＜
，
＞=-
，即＜
，
＞=120°，
∴二面角的大小为60°．
| CA |
| AB |
| AB |
| BD |
| CD |
| CA |
| AB |
| BD |
∴|
| CD |
| CA |
| BD |
| 17 |
∴cos＜
| CA |
| BD |
| 1 |
| 2 |
| CA |
| BD |
∴二面角的大小为60°．
点评：本题主要考查了平面与平面之间的位置关系，考查空间想象能力、运算能力和推理论证能力，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
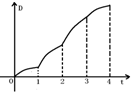
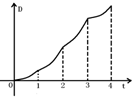
如图放置的边长为1的正方形PABC沿x轴正方向滚动．设顶点P（x，y）的轨迹方程是y=f（x），设y=f（x）在其两个相邻零点间的图象与x轴所围区域为S，则直线x=t从t=0到t=4所匀速移动扫过区域S的面积D与t的函数图象大致为（ ）
