题目内容
将最小正周期为3π的函数f(x)=cos(ωx+φ)-sin(ωx+φ)(ω>0),|φ|<
的图象向左平移
个单位,得到偶函数图象,则φ可能为 .
| π |
| 2 |
| π |
| 4 |
考点:函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:根据f(x)的周期性求得ω=
,可得f(x)=
cos(
x+φ+
),再根据函数y=Acos(ωx+φ)的图象变换规律,余弦函数的图象的对称性,求得φ的值.
| 2 |
| 3 |
| 2 |
| 2 |
| 3 |
| π |
| 4 |
解答:
解:∵f(x)=cos(ωx+φ)-sin(ωx+φ)=
cos(ωx+φ+
)的最小正周期为3π,|
∴
=3π,ω=
,f(x)=
cos(
x+φ+
).
把f(x)的图象向左平移
个单位,得到偶函数y=
cos[
(x+
)+φ+
]=
cos(
x+φ+
)的图象,
可得φ+
=kπ,k∈z.
再结合|φ|<
,可得 φ=-
,
故答案为:-
.
| 2 |
| π |
| 4 |
∴
| 2π |
| ω |
| 2 |
| 3 |
| 2 |
| 2 |
| 3 |
| π |
| 4 |
把f(x)的图象向左平移
| π |
| 4 |
| 2 |
| 2 |
| 3 |
| π |
| 4 |
| π |
| 4 |
| 2 |
| 2 |
| 3 |
| 5π |
| 12 |
可得φ+
| 5π |
| 12 |
再结合|φ|<
| π |
| 2 |
| 5π |
| 12 |
故答案为:-
| 5π |
| 12 |
点评:本题主要考查函数y=Asin(ωx+φ)的图象变换规律,余弦函数的图象的对称性、周期性,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
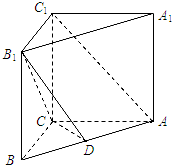 如图,直三棱柱ABC-1B1C1中,AC=4,BC=3,AA1=4,AC⊥BC,点D在线段AB上.
如图,直三棱柱ABC-1B1C1中,AC=4,BC=3,AA1=4,AC⊥BC,点D在线段AB上. 某工厂需要建一个面积为512m2的矩形堆料场,一边可以利用原有的墙壁,为了使砌墙所用的材料最省,则图中的x=
某工厂需要建一个面积为512m2的矩形堆料场,一边可以利用原有的墙壁,为了使砌墙所用的材料最省,则图中的x=