题目内容
下列函数表示同一个函数是（ ）
A、y=x与y=
| ||||||
B、y=
| ||||||
C、y=
| ||||||
D、y=x与y=
|
考点：判断两个函数是否为同一函数
专题：函数的性质及应用
分析：判断函数的定义域与函数的对应法则，即可得到结果．
解答：
解：y=x与y=
两个函数的定义域相同，但是对应法则不同，所以不是相同的函数．
y=
与y=
两个函数的定义域不相同，所以不是相同的函数．
y=
与y=1两个函数的定义域不相同，所以不是相同的函数．
y=x与y=
两个函数的定义域相同，但是对应法则相同，所以是相同的函数．
故选：D．
| x2 |
y=
| x-1 |
| x-1 | ||
|
y=
| x |
| x |
y=x与y=
| 3 | x3 |
故选：D．
点评：本题考查函数的定义域与对应法则的关系，判断函数是否是相同函数的标准．
练习册系列答案
相关题目
问题：
①某社区有500个家庭，其中高收入家庭125户，中等收入家庭280户，低收入家庭95户，为了了解社会购买力的某项指标，要从中抽出一个容量为100户的样本；
②从10名学生中抽出3人参加座谈会．
方法：Ⅰ简单随机抽样法；Ⅱ系统抽样法；Ⅲ分层抽样法；此题中所提问题与抽样方法配对正确的是（ ）
①某社区有500个家庭，其中高收入家庭125户，中等收入家庭280户，低收入家庭95户，为了了解社会购买力的某项指标，要从中抽出一个容量为100户的样本；
②从10名学生中抽出3人参加座谈会．
方法：Ⅰ简单随机抽样法；Ⅱ系统抽样法；Ⅲ分层抽样法；此题中所提问题与抽样方法配对正确的是（ ）
| A、①Ⅲ；②Ⅰ |
| B、①Ⅰ；②Ⅱ |
| C、①Ⅱ；②Ⅲ |
| D、①Ⅲ；②Ⅱ |
若复数z2+2=0，则z3等于（ ）
A、±2
| ||
| B、2 | ||
C、±2
| ||
D、-2
|
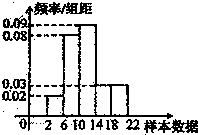若容量为100的某样本的频率分布直方图如图所示，则根据该频率分布直方图可以估计出样本数据落在[14，18）内的频数a的值为（ ）| A、8 | B、12 | C、32 | D、36 |
一个长、宽分别为4和2的长方形内接于圆（如图），质地均匀的一粒石子落入图中（不计边界），则落在长方形内的概率等于（ ）A、
| ||||
B、
| ||||
C、
| ||||
| D、20π |
已知函数y=cos（x-
）的图象为C，为了得到函数y=cos（x+
）的图象只需把C上所有的点（ ）
| 2π |
| 9 |
| 2π |
| 9 |
A、向右平行移动
| ||
B、向左平行移动
| ||
C、向右平行移动
| ||
D、向左平行移动
|