题目内容
设数列{an},如果存在常数a,对于任意给定的正数q(无论多小),总存在正整数M,使得当n>M时,恒有|an-a|<q成立,就称数列{an}为收敛数列,且收敛于a.则下列结论中,正确的是
①等差数列{an}一定不是收敛数列;
②等比数列的公比q满足|q|<1,前n项和为Sn,则数列{Sn}收敛;
③等差数列{an}公差不为0,数列{
}的前n项和为Sn,则数列{Sn}收敛;
④数列{an}的通项公式为an=1+
,则{an}不收敛.
①等差数列{an}一定不是收敛数列;
②等比数列的公比q满足|q|<1,前n项和为Sn,则数列{Sn}收敛;
③等差数列{an}公差不为0,数列{
| 1 |
| anan+1 |
④数列{an}的通项公式为an=1+
| (-1)n |
| n |
考点:命题的真假判断与应用
专题:简易逻辑
分析:首先,准确理解收敛数列的概念,然后,逐个进行判断即可,对于对于①:可以举出特例,例如常数数列则符合收敛的定义;对于对于②:则可以借助于无穷小递缩等比数列的性质求解;对于③:则结合拆项法的思想求解其和,然后判断数列{Sn}的收敛情况;对于④:则利用该数列趋向于1,进行判断其收敛性.
解答:
解:对于①:
若该等差数列为常数列,则符合收敛的条件,
故①错误;
对于②:∵|q|<1,
∴Sn=
→
,
∴数列{Sn}收敛;
对于③:等差数列{an}公差不为0,
设该数列的首项为a1,公差为d,
∴an=a1+(n-1)d=nd+a1-d,
∵
=
(
-
)
∴Sn=
(
-
)+
(
-
)+…+
(
-
)
=
(
-
)
∴Sn→
,
∴数列{Sn}收敛,
故③正确;
对于④:
∵数列{an}的通项公式为an=1+
,
∴an→1,
∴{an}收敛,
故④错误.
故答案为:②③.
若该等差数列为常数列,则符合收敛的条件,
故①错误;
对于②:∵|q|<1,
∴Sn=
| a1(1-qn) |
| 1-q |
| a1 |
| 1-q |
∴数列{Sn}收敛;
对于③:等差数列{an}公差不为0,
设该数列的首项为a1,公差为d,
∴an=a1+(n-1)d=nd+a1-d,
∵
| 1 |
| anan+1 |
| 1 |
| d |
| 1 |
| an |
| 1 |
| an+1 |
∴Sn=
| 1 |
| d |
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| d |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| d |
| 1 |
| an |
| 1 |
| an+1 |
=
| 1 |
| d |
| 1 |
| a1 |
| 1 |
| an+1 |
∴Sn→
| 1 |
| a1d |
∴数列{Sn}收敛,
故③正确;
对于④:
∵数列{an}的通项公式为an=1+
| (-1)n |
| n |
∴an→1,
∴{an}收敛,
故④错误.
故答案为:②③.
点评:本题重点考查了命题的真假判断方法,同时结合数列的有关性质、数列求和思想等,属于中档题.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
下列函数表示同一个函数是( )
A、y=x与y=
| ||||||
B、y=
| ||||||
C、y=
| ||||||
D、y=x与y=
|

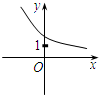 f(x)=ax+b的图象如图,其中a、b为常数,则下列结论正确的是
f(x)=ax+b的图象如图,其中a、b为常数,则下列结论正确的是