题目内容
(本题满分13分)已知数列 满足
满足 .
.
(1)若 ,求证:数列
,求证:数列 是等比数列并求其通项公式;
是等比数列并求其通项公式;
(2)求数列 的通项公式;
的通项公式;
(3)求证: +
+ + +
+ +
 .
.
(1)证明见解析, ;(2)
;(2) ,或
,或 ;(3)见解析
;(3)见解析
【解析】
试题分析:(1)
 又
又
所以 是首项为
是首项为 ,公比为4的等比数列,且
,公比为4的等比数列,且 5分
5分
(2)由(Ⅰ)可知 , 7分
, 7分
 8分
8分
所以 ,或
,或 9分
9分
(3) ∴

 11分
11分
当n=2k时,



当n=2k-1时,

< <3
<3
∴ 13分
13分
考点:本题考查等比数列的定义,等比数列的通项公式,数列的递推公式,数列与不等式的综合

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
 中,若
中,若 ,则
,则 的最小值是 .
的最小值是 .  中,“
中,“ ”是“
”是“ ”的( )
”的( )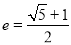 的双曲线
的双曲线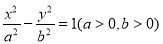 为黄金双曲线.如图是双曲线
为黄金双曲线.如图是双曲线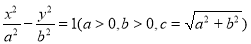 的图象,给出以下几个说法:
的图象,给出以下几个说法: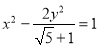 是黄金双曲线;
是黄金双曲线;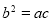 ,则该双曲线是黄金双曲线;
,则该双曲线是黄金双曲线;
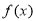 的导函数是
的导函数是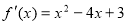 ,则函数
,则函数 (0<a<1)的单调递减区间是( )
(0<a<1)的单调递减区间是( )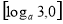 ,
,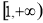

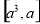

 的值是_____________
的值是_____________

 B.
B. C.
C. D.
D.