题目内容
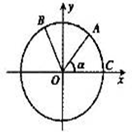如图，点A，B是单位圆O上的两点，点C是圆O与x轴正半轴的交点，将锐角α的终边OA按逆时针方向旋转| π |
| 3 |
（1）若A的坐标为（
| 3 |
| 5 |
| 4 |
| 5 |
（2）求|BC|的取值范围．
考点：任意角的三角函数的定义,三角函数线
专题：三角函数的求值
分析：（1）利用三角函数的定义可得cosα=
，sinα=
，∠COB=α+
，利用两角和的余弦可求得cos（α+
）=
，从而可得点B的横坐标；
（2）先求|BC|2=2-2cos（α+
）的取值范围，再开方即可求得|BC|的取值范围．
| 3 |
| 5 |
| 4 |
| 5 |
| π |
| 3 |
| π |
| 3 |
3-4
| ||
| 10 |
（2）先求|BC|2=2-2cos（α+
| π |
| 3 |
解答：
解：（1）由于A的坐标为（
，
），由三角函数的定义知，cosα=
，sinα=
…2分
又∠COB=α+
，
∴cos（α+
）=cosαcos
-sinαsin
=
…5分
∴点B的横坐标为
…6分
（2）|BC|2=2-2cos（α+
）…9分
∵0＜α＜
，故
＜α+
＜
，
∴cos（α+
）∈（-
，-
），
∴|BC|2∈（1，2+
），
∴|BC|∈（1，
）…12分
| 3 |
| 5 |
| 4 |
| 5 |
| 3 |
| 5 |
| 4 |
| 5 |
又∠COB=α+
| π |
| 3 |
∴cos（α+
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
3-4
| ||
| 10 |
∴点B的横坐标为
3-4
| ||
| 10 |
（2）|BC|2=2-2cos（α+
| π |
| 3 |
∵0＜α＜
| π |
| 2 |
| π |
| 3 |
| π |
| 3 |
| 5π |
| 6 |
∴cos（α+
| π |
| 3 |
| ||
| 2 |
| 1 |
| 2 |
∴|BC|2∈（1，2+
| 3 |
∴|BC|∈（1，
| ||||
| 2 |
点评：本题考查任意角的三角函数的定义，突出考查两角和的余弦与余弦函数的性质，属于中档题．
练习册系列答案
期末1卷素质教育评估卷系列答案
相关题目
直线3x-4y+12=0与圆x2+y2+10x-6y-2=0的位置关系是（ ）
| A、相交 | B、相切 |
| C、相离 | D、相交且过圆心 |
如图为函数y=Asin（ωx+φ）+c（A＞0，ω＞0，0＜φ＜
函数y=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜π）在一个周期内的图象如图，