题目内容
在△ABC中，角A，B，C的对边分别为a，b，c，且a=1，b=
，B=2A．
（1）求cosA的值；
（2）求c的值．
| 3 |
（1）求cosA的值；
（2）求c的值．
考点：余弦定理,正弦定理
专题：三角函数的求值
分析：（1）利用正弦定理列出关系式，将a，b，B=2A代入，计算即可求出cosA的值；
（2）由cosA的值求出A的度数，进而求出B与C的度数，利用正弦定理即可求出c的值．
（2）由cosA的值求出A的度数，进而求出B与C的度数，利用正弦定理即可求出c的值．
解答：
解：（1）在△ABC中，a=1，b=
，B=2A，
由正弦定理
=
得：
=
=
，
则cosA=
；
（2）∵cosA=
，A为三角形内角，
∴A=
，
∴B=2A=
，C=
，
∴由正弦定理
=
得：c=
=2．
| 3 |
由正弦定理
| a |
| sinA |
| b |
| sinB |
| 1 |
| sinA |
| ||
| sin2A |
| ||
| 2sinAcosA |
则cosA=
| ||
| 2 |
（2）∵cosA=
| ||
| 2 |
∴A=
| π |
| 6 |
∴B=2A=
| π |
| 3 |
| π |
| 2 |
∴由正弦定理
| a |
| sinA |
| c |
| sinC |
| asinC |
| sinA |
点评：此题考查了正弦、余弦定理，以及特殊角的三角函数值，熟练掌握定理是解本题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
函数f（x）=（ex+e-x）sinx的部分图象大致为（ ）
A、 |
B、 |
C、 |
D、 |
如图所示的电路图，设命题p：开关K闭合，命题q：开关K1闭合，命题s：开关K2闭合，命题t：开关K3闭合．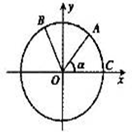
如图，点A，B是单位圆O上的两点，点C是圆O与x轴正半轴的交点，将锐角α的终边OA按逆时针方向旋转