题目内容
 函数y=Asin(ωx+φ)(A>0,ω>0,0<φ<π)在一个周期内的图象如图,
函数y=Asin(ωx+φ)(A>0,ω>0,0<φ<π)在一个周期内的图象如图,(1)求函数的解析式;
(2)求函数的单调区间.
考点:由y=Asin(ωx+φ)的部分图象确定其解析式,函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:(1)直接由图象得到A和半周期,再由周期公式求得ω,利用五点作图的第二点求得φ,则函数解析式可求;
(2)直接利用复合函数的单调性求解单调区间.
(2)直接利用复合函数的单调性求解单调区间.
解答:
解:(1)由图可知A=2,
=
-(-
)=
,T=π.
∴ω=
=2.
由五点作图的第二点知,2×(-
)+φ=
,得:φ=
.
∴y=2sin(2x+
);
(2)由2kπ-
≤2x+
≤2kπ+
,得:
kπ-
≤x≤kπ-
,k∈Z.
∴函数的单调增区间为[kπ-
,kπ-
] (k∈Z);
由2kπ+
≤2x+
≤2kπ+
,得:
kπ-
≤x≤kπ+
,k∈Z.
∴函数的单调减区间为[kπ-
,kπ+
] (k∈Z).
| T |
| 2 |
| 5π |
| 12 |
| π |
| 12 |
| π |
| 2 |
∴ω=
| 2π |
| T |
由五点作图的第二点知,2×(-
| π |
| 12 |
| π |
| 2 |
| 2π |
| 3 |
∴y=2sin(2x+
| 2π |
| 3 |
(2)由2kπ-
| π |
| 2 |
| 2π |
| 3 |
| π |
| 2 |
kπ-
| 7π |
| 12 |
| π |
| 12 |
∴函数的单调增区间为[kπ-
| 7π |
| 12 |
| π |
| 12 |
由2kπ+
| π |
| 2 |
| 2π |
| 3 |
| 3π |
| 2 |
kπ-
| π |
| 12 |
| 5π |
| 12 |
∴函数的单调减区间为[kπ-
| π |
| 12 |
| 5π |
| 12 |
点评:本题考查由函数的部分图象求函数的解析式,关键是会用五点作图的某一点求φ,训练了复合函数的单调性的求法,是中档题.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
已知集合A={x|3≤x≤8},B={x|x2-8x+12<0},则A∩B=( )
| A、{x|2<x≤8} |
| B、{x|2<x≤6} |
| C、{x|3≤x<6} |
| D、{x|6<x≤8} |
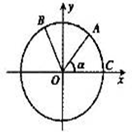 如图,点A,B是单位圆O上的两点,点C是圆O与x轴正半轴的交点,将锐角α的终边OA按逆时针方向旋转
如图,点A,B是单位圆O上的两点,点C是圆O与x轴正半轴的交点,将锐角α的终边OA按逆时针方向旋转 如图在四棱锥P一ABCD中,底面ABCD为直角梯形,AD∥BC,∠BAD=90°.BC=2AD,AC与BD交于点O,点M,N分别在线PC、AB上,
如图在四棱锥P一ABCD中,底面ABCD为直角梯形,AD∥BC,∠BAD=90°.BC=2AD,AC与BD交于点O,点M,N分别在线PC、AB上,