题目内容
已知公差大于0的等差数列{an},a2=4,且a2,a4-2,a6成等比数列.
(1)求数列{an}的通项公式;
(2)数列{bn}的通项公式是bn=2an,求数列{bn}的前n项和Sn.
(1)求数列{an}的通项公式;
(2)数列{bn}的通项公式是bn=2an,求数列{bn}的前n项和Sn.
考点:数列的求和,等比数列的性质
专题:等差数列与等比数列
分析:(1)由题意列出方程解得d,写出通项公式;
(2)易得数列{bn}是首项为2,公比为8的等比数列,利用前n项和公式求出数列{bn}的前n项和Sn.
(2)易得数列{bn}是首项为2,公比为8的等比数列,利用前n项和公式求出数列{bn}的前n项和Sn.
解答:
解:(1)设等差数列的公差为d,由题意得(a4-2)2=a2a6
即(4+2d-2)2=4(4+4d),解得d=3或d=-1(舍去)
∴an=3n-2.
(2)由(1)得bn=2an=23n-2=2•8n-1,
∴数列{bn}是首项为2,公比为8的等比数列,
∴sn=
=
(8n-1).
即(4+2d-2)2=4(4+4d),解得d=3或d=-1(舍去)
∴an=3n-2.
(2)由(1)得bn=2an=23n-2=2•8n-1,
∴数列{bn}是首项为2,公比为8的等比数列,
∴sn=
| 2(1-8n) |
| 1-8 |
| 2 |
| 7 |
点评:本题考查等差数列及等比数列的有关性质的应用,注意方程思想的运用,属中档题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
已知M={x|x=2m-1,m∈Z},N={x|x2-x-12<0,x∈R},则集合M∩N等于( )
| A、{-3,-1,1,3} |
| B、{1,3} |
| C、{0,1,2,3} |
| D、{-1,1,3} |
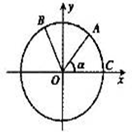 如图,点A,B是单位圆O上的两点,点C是圆O与x轴正半轴的交点,将锐角α的终边OA按逆时针方向旋转
如图,点A,B是单位圆O上的两点,点C是圆O与x轴正半轴的交点,将锐角α的终边OA按逆时针方向旋转 如图在四棱锥P一ABCD中,底面ABCD为直角梯形,AD∥BC,∠BAD=90°.BC=2AD,AC与BD交于点O,点M,N分别在线PC、AB上,
如图在四棱锥P一ABCD中,底面ABCD为直角梯形,AD∥BC,∠BAD=90°.BC=2AD,AC与BD交于点O,点M,N分别在线PC、AB上,