题目内容
甲有三本不同的书，乙去借阅，并且至少借1本，则不同借法的总数为 ．（用数字作答）
考点：排列、组合及简单计数问题
专题：排列组合
分析：只借一本的方法种数，只借2本的方法种数，三本不同的书全借的方法种数，把这三个结果相加，即得所求．
解答：
解：只借一本的方法种数为 C31=3，
只借2本的方法种数为 C32=3，
三本不同的书全借的方法种数为1，
∴至少借一本的方法有 3+3+1=7 种，
故答案为：7．
只借2本的方法种数为 C32=3，
三本不同的书全借的方法种数为1，
∴至少借一本的方法有 3+3+1=7 种，
故答案为：7．
点评：本题考查排列与组合及两个基本原理，组合数公式的应用，体现了分类讨论的数学思想，分类讨论是解题的关键．
练习册系列答案
互动英语系列答案
相关题目
已知函数f（x）=x3+3x（x≥0），对于曲线y=f（x）上横坐标成公差为1的等差数列的三个点A，B，C，给出以下判断：①△ABC一定是钝角三角形；
②△ABC可能是直角三角形；
③△ABC可能为锐角三角形；
④△ABC不可能是等腰三角形，其中所有正确的序号是（ ）
②△ABC可能是直角三角形；
③△ABC可能为锐角三角形；
④△ABC不可能是等腰三角形，其中所有正确的序号是（ ）
| A、①② | B、①③ | C、②③ | D、①④ |
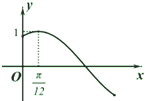已知函数f（x）=sin（2x+φ）（0＜φ＜π）的部分图象，如图所示，则φ=（ ）A、
| ||
B、
| ||
C、
| ||
D、
|