题目内容
若函数f（x）=ax3+3x2-x恰好有三个单调区间，那么a的取值范围是 ．
考点：利用导数研究函数的极值
专题：分类讨论,导数的综合应用
分析：求出函数的导函数，利用导数有两个不同的零点，说明函数恰好有三个单调区间，从而求出a的取值范围．
解答：
解：∵函数f（x）=ax3+3x2-x，
∴f′（x）=3ax2+6x-1，
由函数f（x）恰好有三个单调区间，得f′（x）有两个不相等的零点，
∴3ax2+6x-1=0满足：a≠0，且△=36+12a＞0，解得a＞-3，
∴a∈（-3，0）∪（0，+∞）．
故答案为：（-3，0）∪（0，+∞）．
∴f′（x）=3ax2+6x-1，
由函数f（x）恰好有三个单调区间，得f′（x）有两个不相等的零点，
∴3ax2+6x-1=0满足：a≠0，且△=36+12a＞0，解得a＞-3，
∴a∈（-3，0）∪（0，+∞）．
故答案为：（-3，0）∪（0，+∞）．
点评：本题考查导数在研究函数单调性的应用，运用了分类讨论思想，方程思想．属于中档题．
练习册系列答案
相关题目
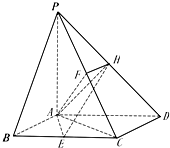如图，四棱锥P-ABCD的底面是菱形，∠ABC=60°，PA⊥底面ABCD，E，F分别是BC，PC的中点，点H在PD上，且EH⊥PD，PA=AB=2．