题目内容
定义行列式运算
=a1a4-a2a3.将函数f(x)=
图象向左平移
个单位后,所得函数图象的一条对称轴是( )
|
|
| π |
| 6 |
A、x=
| ||
B、x=
| ||
C、x=
| ||
D、x=
|
考点:函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:由新定义化简函数f(x)的解析式,然后以x+
替换x,再由所得角的终边落在y轴上求得函数的一条对称轴方程.
| π |
| 6 |
解答:
解:由定义的行列式运算可知,
f(x)=
=(1+sin2x)sin2x-cos2x(-cos2x)
=sin2x+sin22x+cos22x
=sin2x+1.
将函数f(x)的图象向左平移
个单位后,得到的函数解析式为y=sin2(x+
)+1.
由2(x+
)=kπ+
,k∈Z,
得x=
+
,k∈Z.
∴当k=0时,x=
.
∴所得函数图象的一条对称轴是x=
.
故选:D.
f(x)=
|
=(1+sin2x)sin2x-cos2x(-cos2x)
=sin2x+sin22x+cos22x
=sin2x+1.
将函数f(x)的图象向左平移
| π |
| 6 |
| π |
| 6 |
由2(x+
| π |
| 6 |
| π |
| 2 |
得x=
| kπ |
| 2 |
| π |
| 12 |
∴当k=0时,x=
| π |
| 12 |
∴所得函数图象的一条对称轴是x=
| π |
| 12 |
故选:D.
点评:本题考查了y=Asin(ωx+φ)型函数的图象变换,三角函数的平移原则为左加右减上加下减,考查了三角函数对称轴方程的求法,是中档题.

练习册系列答案
相关题目
函数y=3x+1(x≥-1)的值域是( )
| A、(0,+∞) |
| B、(1,+∞) |
| C、[0.+∞) |
| D、[1.+∞) |
已知α为第二象限角,tanα=-2,则cosα=( )
A、
| ||||
B、-
| ||||
C、-
| ||||
D、
|
执行如图的程序,若输出结果为2,则输入的实数x的值是( )


| A、3 | ||
B、
| ||
| C、4 | ||
| D、2 |
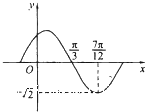 函数f(x)=Asin(ωx+φ)(A,ω,φ为常数,A>0,ω>0)的部分图象如图所示,则Atanφ的值为( )
函数f(x)=Asin(ωx+φ)(A,ω,φ为常数,A>0,ω>0)的部分图象如图所示,则Atanφ的值为( )A、-
| ||
B、-
| ||
C、
| ||
D、
|
要得到函数y=cos3x的图象,只需将函数y=sin3x的图象( )
A、右移
| ||
B、左移
| ||
C、右移
| ||
D、左移
|
设α﹑β为钝角,且sinα=
,cosβ=-
,则α+β的值为( )
| ||
| 5 |
3
| ||
| 10 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|