题目内容
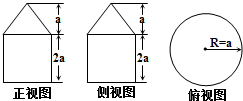 已知一个几何体的三视图如图所示,则此几何体的侧面积是( )
已知一个几何体的三视图如图所示,则此几何体的侧面积是( )| A、4πa2 | ||
| B、5πa2 | ||
C、(4+
| ||
D、(5+
|
考点:组合几何体的面积、体积问题
专题:空间位置关系与距离
分析:由几何体的三视图可知,该几何体是一组合体,上部为圆锥,下部为圆柱.直接求解侧面积即可.
解答:
解:由几何体的三视图可知,该几何体是一组合体,上部为圆锥,下部为圆柱.
底面直径为2a,圆锥高为a,侧面积为:πrl=
πa2.
圆柱高为2a,侧面积为:2πrl=2π×a×2a=4πa2.
组合体的侧面积为:(4+
)πa2.
故选:C.
底面直径为2a,圆锥高为a,侧面积为:πrl=
| 2 |
圆柱高为2a,侧面积为:2πrl=2π×a×2a=4πa2.
组合体的侧面积为:(4+
| 2 |
故选:C.
点评:本题考查由三视图求几何体的体积,考查由三视图还原几何体直观图,考查圆锥、柱体的体积公式,本题是一个基础题.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
已知集合M={x|x2-2x-3≤0},N={x|y=
},则M∩N=( )
| x-2 |
| A、{x|-1≤x≤3} |
| B、{x|2≤x≤3} |
| C、{x|-1≤x≤2} |
| D、∅ |
如图所示,程序框图的输出结果是( )


| A、13 | B、14 | C、16 | D、15 |
“a>2”是“函数f(x)=loga(2-ax)在定义域内为减函数”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
下列命题或等式正确的是( )
| A、若f(x)是奇函数,则f(0)=0 | ||
B、∫
| ||
| C、函数f(x)=cos2x是周期为π的减函数 | ||
| D、若a∈R,则“a2<a”是“a>0”的必要条件 |
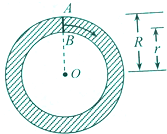 如图,我们知道,圆环也可看作线段AB绕圆心O旋转一周所形成的平面图形,又圆环的面积S=π(R2-r2)=(R-r)×2π×
如图,我们知道,圆环也可看作线段AB绕圆心O旋转一周所形成的平面图形,又圆环的面积S=π(R2-r2)=(R-r)×2π×