题目内容
过双曲线x2-
=1的左焦点F1作直线l与双曲线相交于A、B两点,记|AB|=m,若从区间(2,8)中任取一个实数为m,则这样的直线l恰好能作两条的概率为 .
| y2 |
| 3 |
考点:古典概型及其概率计算公式
专题:概率与统计
分析:双曲线的两个顶点之间的距离是2,过抛物线的焦点一定有两条直线使得交点之间的距离等于m,当直线与实轴垂直时,做出直线与双曲线交点的纵标,得到也是一条长度等于m的线段.
解答:
解:双曲线为:x2-
=1,则a=1,b=
;
若AB只与双曲线右支相交时,|AB|的最小距离是通径,长度为
=6,
此时只有一条直线符合条件;
若AB与双曲线的两支都相交时,此时|AB|的最小距离是实轴两顶点的距离,长度为2a=2,距离无最大值,
结合双曲线的对称性,可得此时有2条直线符合条件;
综合可得,有3条直线符合条件;
故直线l恰好能作两条的概率为:
.
故答案为:
.
| y2 |
| 3 |
| 3 |
若AB只与双曲线右支相交时,|AB|的最小距离是通径,长度为
| 2b2 |
| a |
此时只有一条直线符合条件;
若AB与双曲线的两支都相交时,此时|AB|的最小距离是实轴两顶点的距离,长度为2a=2,距离无最大值,
结合双曲线的对称性,可得此时有2条直线符合条件;
综合可得,有3条直线符合条件;
故直线l恰好能作两条的概率为:
| 2 |
| 3 |
故答案为:
| 2 |
| 3 |
点评:本题考查直线与双曲线之间的关系问题,几何概型的概率计算,以及思路是先求得试验的全部构成的长度和构成事件的区域长度,再求比值,本题解题的关键是看清楚当直线的斜率不存在,即直线与实轴垂直时,要验证线段的长度,属于中档题.

练习册系列答案
相关题目
已知集合M={x|x2-2x-3≤0},N={x|y=
},则M∩N=( )
| x-2 |
| A、{x|-1≤x≤3} |
| B、{x|2≤x≤3} |
| C、{x|-1≤x≤2} |
| D、∅ |

 如图根据频率分布直方图估计该组数据的中位数是
如图根据频率分布直方图估计该组数据的中位数是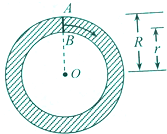 如图,我们知道,圆环也可看作线段AB绕圆心O旋转一周所形成的平面图形,又圆环的面积S=π(R2-r2)=(R-r)×2π×
如图,我们知道,圆环也可看作线段AB绕圆心O旋转一周所形成的平面图形,又圆环的面积S=π(R2-r2)=(R-r)×2π×