题目内容
（1）计算log3
+lg25+lg4+7log72的值；
（2）已知函数f（x）=
，求f（-4）、f（3）、f[f（-2）]的值．
| |||
| 3 |
（2）已知函数f（x）=
|
考点：对数的运算性质,函数的值
专题：计算题
分析：（1）化根式为分数指数幂，然后直接利用对数的运算性质求解；
（2）直接把x的值代入分段函数求解函数值．
（2）直接把x的值代入分段函数求解函数值．
解答：
解：（1）log3
+lg25+lg4+7log72
=log3
+lg(4×25)+2
=log33-
+lg102+2
=-
+2+2
=
；
（2）∵f(x)=
，
∴f（-4）=-4+2=-2，f（3）=2×3=6，
f（-2）=0，f[f（-2）]=f（0）=0．
| |||
| 3 |
=log3
3
| ||
| 3 |
=log33-
| 1 |
| 4 |
=-
| 1 |
| 4 |
=
| 15 |
| 4 |
（2）∵f(x)=
|
∴f（-4）=-4+2=-2，f（3）=2×3=6，
f（-2）=0，f[f（-2）]=f（0）=0．
点评：本题考查了对数的运算性质，考查了分段函数的函数值的求法，是基础的计算题．
练习册系列答案
相关题目
直线L1过点A（m，1）和点B（-1，m），直线L2过点C（m+n，n+1）和点D（n+1，n-m）．则直线L1与L2的位置关系是（ ）
| A、重合 | B、平行 |
| C、垂直 | D、无法确定 |
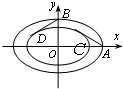简化北京奥动会主体育场“鸟巢”的钢结构俯视图如图所示，内外两圈的钢骨架是离心率相同的椭圆，外层椭圆顶点向内层椭圆引切线AC、BD，设内层椭圆方程为
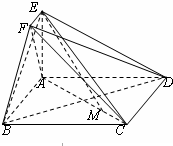在如图所示的几何体中，四边形ABCD为正方形，EA⊥平面ABCD，EF∥AB，AB=4，AE=2，EF=1．