题目内容
直线L1过点A(m,1)和点B(-1,m),直线L2过点C(m+n,n+1)和点D(n+1,n-m).则直线L1与L2的位置关系是( )
| A、重合 | B、平行 |
| C、垂直 | D、无法确定 |
考点:两条直线平行与倾斜角、斜率的关系
专题:直线与圆
分析:分类讨论两条直线的斜率与垂直的位置关系即可得出.
解答:
解:①当m=1时,直线L1过点A(1,1)和点B(-1,1),直线L2过点C(1+n,n+1)和点D(n+1,n-1).
此时直线L1的斜率k1=0,直线L2的斜率不存在,因此L1⊥L2.
②当m=-1时,直线L1过点A(-1,1)和点B(-1,-1),直线L2过点C(-1+n,n+1)和点D(n+1,n+1).
此时直线L1的斜率不存在,直线L2的斜率k2=0,因此L1⊥L2.
②当m≠±1时,直线L1的斜率k1=
,直线L2的斜率k2=
.
此时k1•k2=-1,∴L1⊥L2.
综上可知:直线L1与L2的位置关系是垂直.
故选:C.
此时直线L1的斜率k1=0,直线L2的斜率不存在,因此L1⊥L2.
②当m=-1时,直线L1过点A(-1,1)和点B(-1,-1),直线L2过点C(-1+n,n+1)和点D(n+1,n+1).
此时直线L1的斜率不存在,直线L2的斜率k2=0,因此L1⊥L2.
②当m≠±1时,直线L1的斜率k1=
| m-1 |
| -1-m |
| -m-1 |
| 1-m |
此时k1•k2=-1,∴L1⊥L2.
综上可知:直线L1与L2的位置关系是垂直.
故选:C.
点评:本题考查了两条直线的斜率与垂直的关系、分类讨论,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知a=log45,b=4-
,c=sin2,则a、b、c的大小关系是( )
| 1 |
| 2 |
| A、b<c<a |
| B、c<a<b |
| C、a<b<c |
| D、c<b<a |
圆心在直线y=-4x上,且与直线l:x+y-1=0相切于点P(3,-2)的圆的方程是( )
| A、(x-1)2+(y+4)2=8 |
| B、(x-3)2+(y-1)2=9 |
| C、(x+1)2+(y-3)2=5 |
| D、(x-1)2+(y-5)2=16 |
在△ABC中,边a,b,c的对角分别为A,B,C,若a2=b2+c2+
bc,则A的大小为( )
| 3 |
| A、30° | B、60° |
| C、120° | D、150° |
等比数列{an}的前n项和为Sn,若a1+a2+a3=3,a4+a5+a6=6,则S12=( )
| A、15 | B、30 | C、45 | D、60 |
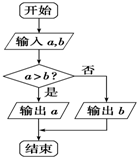 如图所示的程序框图,其功能是( )
如图所示的程序框图,其功能是( )| A、输入a,b的值,按从小到大的顺序输出它们的值 |
| B、输入a,b的值,按从大到小的顺序输出它们的值 |
| C、求a,b的最大值 |
| D、求a,b的最小值 |
关于x的方程
sin2x+cos2x=k+1在[0,
]内有两相异实根,则k满足( )
| 3 |
| π |
| 2 |
| A、k∈(-3,1) |
| B、k∈[0,1) |
| C、k∈(-2,1) |
| D、k∈(0,1) |
已知α,β均为锐角,且3sinα=2sinβ,3cosα+2cosβ=3,则α+2β的值为( )
A、
| ||
B、
| ||
C、
| ||
| D、π |