Question

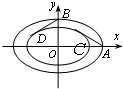简化北京奥动会主体育场“鸟巢”的钢结构俯视图如图所示，内外两圈的钢骨架是离心率相同的椭圆，外层椭圆顶点向内层椭圆引切线AC、BD，设内层椭圆方程为

x2

a2

+

y2

b2

=1(a＞b＞0)，则外层椭圆方程可设为

x2

(ma)2

+

y2

(mb)2

=1(a＞b＞0，m＞1)，若AC与BD的斜率之积为-

9

25

，则椭圆的离心率为（　　）

• A、

  4

  5

• B、

  1

  2

• C、

  3

  5

• D、

  3

  4

Answer 1

考点：椭圆的应用

专题：综合题,圆锥曲线的定义、性质与方程

分析：设出切线AC和BD的方程，与椭圆方程联立消去y，根据判别式等于0求得k₁和k₂的表达式，根据AC与BD的斜率之积求得a和b的关系，进而求得a和c的关系，椭圆的离心率可得．

解答： 解：设切线AC的方程为y=k₁（x-ma），代入

x2

a2

+

y2

b2

=1(a＞b＞0)，
消去y得（b²+a²k₁²）x²-2ma³k₁²x+m²a⁴k₁²-a²b²=0
由△=0⇒k₁²=

b2

a2

•

1

m2-1

，同理k₂²=

b2

a2

•（m²-1）
∴k₁²•k₂²=

b4

a4

，
∵AC与BD的斜率之积为-

9

25

，
∴

b2

a2

=

9

25

，
∴e=

c

a

=

a2-b2 a2

=

4

5

，
故选A．

点评：本题主要考查了椭圆的简单性质和直线与椭圆的位置关系，考查了学生综合分析问题和解决问题的能力，属于中档题．