题目内容
11.利用单调性定义判断函数f(x)=$\frac{x-2}{x-1}$(x∈[2,6])是增函数还是减函数,并求出最值.分析 函数f(x)=$\frac{x-2}{x-1}$=1-$\frac{1}{x-1}$(x∈[2,6])是增函数,利用定义法能进行证明,根据函数的单调性能求出最值.
解答 解:函数f(x)=$\frac{x-2}{x-1}$=1-$\frac{1}{x-1}$(x∈[2,6])是增函数.
证明如下:
在[2,6]内任取x1,x2,令x1<x2,
f(x1)-f(x2)=(1-$\frac{1}{{x}_{1}-1}$)-(1-$\frac{1}{{x}_{2}-1}$)=$\frac{1}{{x}_{2}-1}-\frac{1}{{x}_{1}-1}$,
∵x1,x2∈[2,6],x1<x2,
∴f(x1)-f(x2)=$\frac{1}{{x}_{2}-1}-\frac{1}{{x}_{1}-1}$<0,即f(x1)<f(x2),
∴函数f(x)=$\frac{x-2}{x-1}$(x∈[2,6])是增函数.
∴f(x)min=f(2)=0,$f(x)_{max}=f(6)=\frac{6-2}{6-1}$=$\frac{4}{5}$.
∴f(x)在[2,6]上的最小值为0,最大值为$\frac{4}{5}$.
点评 本题考查函数的单调性的判断与证明,考查最值的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案
相关题目
6.设向量$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为θ,则“$\overrightarrow{a}$•$\overrightarrow{b}$<0”是“θ为钝角”的( )
| A. | 充分不必要条件 | B. | 必要不充分 | ||
| C. | 充要条件 | D. | 既不充分也不必要 |
3.已知数列{an}为等差数列,Sn为前n项和,公差为d,若$\frac{{S}_{2017}}{2017}$-$\frac{{S}_{17}}{17}$=100,则d的值为( )
| A. | $\frac{1}{20}$ | B. | $\frac{1}{10}$ | C. | 10 | D. | 20 |
20.运行如图算法语句时,输出的数=( )


| A. | 10 | B. | 4 | C. | 6 | D. | 15 |
1.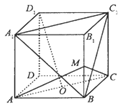 如图,正方体ABCD-A1B1C1D1中,O为底面ABCD的中心,M为棱BB1的中点,则下列结论中错误的是( )
如图,正方体ABCD-A1B1C1D1中,O为底面ABCD的中心,M为棱BB1的中点,则下列结论中错误的是( )
 如图,正方体ABCD-A1B1C1D1中,O为底面ABCD的中心,M为棱BB1的中点,则下列结论中错误的是( )
如图,正方体ABCD-A1B1C1D1中,O为底面ABCD的中心,M为棱BB1的中点,则下列结论中错误的是( )| A. | D1O∥平面A1BC1 | B. | D1O⊥平面MAC | ||
| C. | 异面直线BC1与AC所成的角为60° | D. | MO与底面所成角为90° |
 公路陡坡警示牌如图所示,其中“3.8%”表示这段道路的横截面斜坡所在直线的斜率,这段斜坡的倾斜角的大小为arctan0.038度.(答案保留整数)
公路陡坡警示牌如图所示,其中“3.8%”表示这段道路的横截面斜坡所在直线的斜率,这段斜坡的倾斜角的大小为arctan0.038度.(答案保留整数)