题目内容
8. 如图,四边形ABCD是平行四边形,平面AED⊥平面ABCD,EF∥AB,$BC=EF=\frac{1}{2}AB$,∠BAD=60°,G为BC的中点.
如图,四边形ABCD是平行四边形,平面AED⊥平面ABCD,EF∥AB,$BC=EF=\frac{1}{2}AB$,∠BAD=60°,G为BC的中点.(Ⅰ)求证:FG∥平面BED;
(Ⅱ)求证:平面BED⊥平面AED.
分析 (1)令BD中点为O,连结GO,EO,只需证明FG∥EO即可,
(2)只需证明BD⊥面EAD即可.
解答 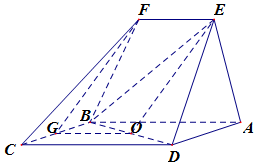 解:(1)令BD中点为O,∵GO∥AB,且$GO=\frac{1}{2}AB$,EF∥AB,且$EF=\frac{1}{2}AB$,
解:(1)令BD中点为O,∵GO∥AB,且$GO=\frac{1}{2}AB$,EF∥AB,且$EF=\frac{1}{2}AB$,
∴GO∥EF,且GO=EF,四边形GOEF是平行四边形,得FG∥EO,
又∵FG?面BED,EO?面BED,∴FG∥面BED.
(2)∵$∠BAO={60°},BC=\frac{1}{2}AB$,
∴∠BDA=90°,即BD⊥AD;
又∵面AED⊥面ABCD,且交线为AD,
∴BD⊥面EAD,面BED⊥面EAD.
点评 本题考查了线面平行,面面垂直的判定,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.已知等比数列{an}的前n项和为Sn,若$\frac{S_4}{a_4}=\frac{S_2}{a_2}$,则$\frac{{{S_{2016}}}}{S_1}$等于( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2016 |
19.若平面α⊥平面β,且平面α内的一条直线a垂直于平面β内的一条直线b,则( )
| A. | 直线a必垂直于平面β | B. | 直线b必垂直于平面α | ||
| C. | 直线a不一定垂直于平面β | D. | 过a的平面与过b的平面垂直 |
3.已知直线m,n和平面α,下列推理正确的是( )
| A. | $\left.{\begin{array}{l}{m⊥n}\\{n?α}\end{array}}\right\}⇒m⊥α$ | B. | $\left.{\begin{array}{l}{m⊥n}\\{n⊥α}\end{array}}\right\}⇒m∥α$ | C. | $\left.{\begin{array}{l}{m⊥α}\\{n∥α}\end{array}}\right\}⇒m⊥n$ | D. | $\left.{\begin{array}{l}{m∥α}\\{n?α}\end{array}}\right\}⇒m∥n$ |
20.为了得到函数y=sin3x-$\sqrt{3}$cos3x的图象( )
| A. | 只要将函数y=2sin3x的图象向右平移$\frac{π}{3}$个单位 | |
| B. | 只要将函数y=sin3x的图象向右平移$\frac{π}{3}$个单位 | |
| C. | 只要将函数y=2sin3x的图象向右平移$\frac{π}{9}$个单位 | |
| D. | 只要将函数y=sin3x的图象向右平移$\frac{π}{9}$个单位 |
18.已知函数$f(x)=\left\{\begin{array}{l}lnx,x>1\\{2^{-x+1}},x≤1\end{array}\right.$,若方程$f(x)-ax=\frac{5}{2}$有3个不同的解,则a的取值范围是( )
| A. | $(-∞,-\frac{5}{2}]$ | B. | $(-\frac{5}{2},-\frac{3}{2}]$ | C. | $[-\frac{5}{2},-\frac{3}{2}]$ | D. | $(-\frac{3}{2},+∞)$ |
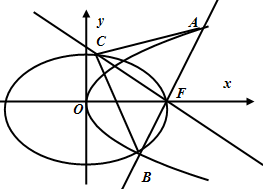 如图,设椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),长轴的右端点与抛物线C2:y2=8x的焦点F重合,且椭圆C1的离心率是$\frac{\sqrt{3}}{2}$.
如图,设椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),长轴的右端点与抛物线C2:y2=8x的焦点F重合,且椭圆C1的离心率是$\frac{\sqrt{3}}{2}$.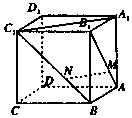 正方体ABCD-A1B1C1D1中,点M、N分别在线段AB1、BC1上,且AM=BN.以下结论:①AA1⊥MN;②A1C1∥MN;③MN∥平面A1B1C1D1;④MN与A1C1异面,⑤MN与 A1C1成30°.其中有可能成立的结论的个数为( )
正方体ABCD-A1B1C1D1中,点M、N分别在线段AB1、BC1上,且AM=BN.以下结论:①AA1⊥MN;②A1C1∥MN;③MN∥平面A1B1C1D1;④MN与A1C1异面,⑤MN与 A1C1成30°.其中有可能成立的结论的个数为( )