函数$y=\sqrt{1-{2^x}}$的定义域是( )A．(-∞.0]B．[0.+∞)C．[1.+∞)D．(-∞.1] 题目和参考答案——青夏教育精英家教网——

题目内容

3．函数$y=\sqrt{1-{2^x}}$的定义域是（　　）

A．

（-∞，0]

B．

[0，+∞）

C．

[1，+∞）

D．

（-∞，1]

分析根据二次根式的性质求出x的范围即可．

解答解：由题意得：
1-2^x≥0，解得：x≤0，
故函数的定义域是（-∞，0]，
故选：A．

点评本题考查了求函数的定义域问题，考查指数的运算，是一道基础题．

练习册系列答案

德华书业寒假训练营学年总复习安徽文艺出版社系列答案

阳光假日寒假系列答案

蓝天教育寒假优化学习系列答案

寒假专题集训系列答案

步步高寒假专题突破练黑龙江出版社系列答案

寒假自主学习手册系列答案

寒假总动员合肥工业大学出版社系列答案

寒假最佳学习方案寒假作业系列答案

寒假作业长江出版社系列答案

寒假作业黄山书社系列答案

相关题目

已知函数f（x）=$\left\{\begin{array}{l}ax+b，x＜0\\{2^x}，x≥0\end{array}\right.$，且f（-2）=3，f（-1）=f（1）．
（Ⅰ）求f（x）的解析式，并求f（f（-2））的值；
（Ⅱ）请在给定的直角坐标系内，利用“描点法”画出y=f（x）的大致图象．

14．不等式2^2x-1＜2的解集是（　　）

11．数列{a_n}满足a₁=2，${a_{n+1}}=\frac{{1+{a_n}}}{{1-{a_n}}}（n∈{N^*}）$，则a₆=-3．

18．已知等比数列{a_n}的前n项和为S_n，若$\frac{S_4}{a_4}=\frac{S_2}{a_2}$，则$\frac{{{S_{2016}}}}{S_1}$等于（　　）

8．若函数f（x）的定义域为[1，2]，则函数y=f（x²）的定义域为（　　）

[1，$\sqrt{2}$]

[-$\sqrt{2}$，$\sqrt{2}$]

[-$\sqrt{2}$，-1]∪[1，$\sqrt{2}$]

15．已知函数f（x）是定义在R上的奇函数，且当x＞0时，$f（x）={（\frac{1}{3}）^x}$
（1）求函数f（x）的解析式；
（2）直接写出单调区间，并计算f（log₃2+1）的值．

如图，在平行六面体ABCD-A₁B₁C₁D₁中，M，N分别在面对角线AC，A₁C上且CM=2MA，A₁N=2ND．记向量$\overrightarrow{AB}=\overrightarrow a，\overrightarrow{AD}=\overrightarrow b，\overrightarrow{A{A_1}}=\overrightarrow c$，用$\overrightarrow a，\overrightarrow b，\overrightarrow c$表示$\overrightarrow{MN}$．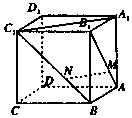

正方体ABCD-A₁B₁C₁D₁中，点M、N分别在线段AB₁、BC₁上，且AM=BN．以下结论：①AA₁⊥MN；②A₁C₁∥MN；③MN∥平面A₁B₁C₁D₁；④MN与A₁C₁异面，⑤MN与 A₁C₁成30°．其中有可能成立的结论的个数为（　　）