题目内容
10.集合M={y|y=-x2,x∈R},N={x|x2+y2=2,x∈R},则M∩N=( )| A. | {(-1,-1),(1,-1)} | B. | {-1} | C. | [-1,0] | D. | [-$\sqrt{2}$,0] |
分析 由二次函数的值域求出集合M,由条件和圆的性质求出集合N,由交集的运算求出M∩N.
解答 解:由y=-x2(x∈R)得y≤0,则集合M={y|y=-x2,x∈R}=(-∞,0],
由x2+y2=2(x∈R)得$-\sqrt{2}≤x≤\sqrt{2}$,则N={x|x2+y2=2,x∈R}=[$-\sqrt{2}$,$\sqrt{2}$],
所以M∩N=[$-\sqrt{2}$,0],
故选D.
点评 本题考查交集及其运算,二次函数的值域,以及圆的性质,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.关于下面等高条形图说法正确的有( )
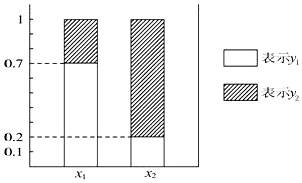

| A. | 在被调查的 x 1中,y 1占70% | B. | 在被调查的 x 2中,y 2占20% | ||
| C. | x 1与 y 1有关 | D. | 以上都不对 |
15.已知双曲线的中心在原点,两个焦点F1,F2分别为$(-\sqrt{5},0)和(\sqrt{5},0)$,点P在双曲线上,PF1⊥PF2,且△PF1F2的面积为1,则双曲线的方程为( )
| A. | $\frac{x^2}{2}-\frac{y^2}{3}=1$ | B. | $\frac{x^2}{3}-\frac{y^2}{2}=1$ | C. | $\frac{x^2}{4}-{y^2}=1$ | D. | ${x^2}-\frac{y^2}{4}=1$ |
2.已知i是复数的虚数单位,若复数z(1+i)=|2i|,则复数z=( )
| A. | 1-i | B. | -1+i | C. | 1+i | D. | i |
20.已知命题p:“?x∈R,x2-2x+2>0”,则¬p是( )
| A. | ?x∈R,x2-2x+2≤0 | B. | ?x0∈R,$x_0^2-2{x_0}+2>0$ | ||
| C. | ?x0∈R,$x_0^2-2{x_0}+2<0$ | D. | ?x0∈R,$x_0^2-2{x_0}+2≤0$ |
 如图所示,在△ABC中,I为△ABC的内心,AI交BC于D,交△ABC外接圆于E
如图所示,在△ABC中,I为△ABC的内心,AI交BC于D,交△ABC外接圆于E