题目内容
15.已知双曲线的中心在原点,两个焦点F1,F2分别为$(-\sqrt{5},0)和(\sqrt{5},0)$,点P在双曲线上,PF1⊥PF2,且△PF1F2的面积为1,则双曲线的方程为( )| A. | $\frac{x^2}{2}-\frac{y^2}{3}=1$ | B. | $\frac{x^2}{3}-\frac{y^2}{2}=1$ | C. | $\frac{x^2}{4}-{y^2}=1$ | D. | ${x^2}-\frac{y^2}{4}=1$ |
分析 利用△PF1F2的面积为1,PF1⊥PF2,可得|PF1|•|PF2|=2,利用勾股定理,结合双曲线的定义,即可求双曲线的方程.
解答 解:由题意,c=$\sqrt{5}$,
因为△PF1F2的面积为1,PF1⊥PF2,
所以|PF1|•|PF2|=2,
又|PF1|2+|PF2|2=|F1F2|2=4c2=20,
从而(|PF1|-|PF2|)2=|PF1|2+|PF2|2-2|PF1|•|PF2|=20-4=16,即4a2=16,a=2,
所以b2=c2-a2=5-4=1,
所以双曲线的方程为$\frac{{x}^{2}}{4}$-y2=1,
故选:C.
点评 本题考查双曲线的标准方程,考查勾股定理,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
5.已知A(1,0,0)、B(0,1,0)、C(0,0,1),则平面ABC的一个单位法向量是( )
| A. | ($\frac{\sqrt{3}}{3}$,$\frac{\sqrt{3}}{3}$,-$\frac{\sqrt{3}}{3}$) | B. | ($\frac{\sqrt{3}}{3}$,-$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{3}}{3}$) | C. | (-$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{3}}{3}$) | D. | (-$\frac{\sqrt{3}}{3}$,-$\frac{\sqrt{3}}{3}$,-$\frac{\sqrt{3}}{3}$) |
10.集合M={y|y=-x2,x∈R},N={x|x2+y2=2,x∈R},则M∩N=( )
| A. | {(-1,-1),(1,-1)} | B. | {-1} | C. | [-1,0] | D. | [-$\sqrt{2}$,0] |
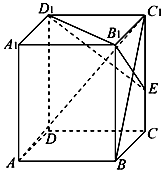 在长方体ABCD-A1B1C1D1中,已知AB=BC=2,BB1=3,连接BC1,过B1作B1E⊥BC1交CC1于点E.
在长方体ABCD-A1B1C1D1中,已知AB=BC=2,BB1=3,连接BC1,过B1作B1E⊥BC1交CC1于点E.